Question

12．某校高一年级学生全部参加了体育科目的达标测试，现从中随机抽取40名学生的测试成绩，整理数据并按分数段[40，50），[50，60），[60，70），[70，80），[80，90），[90，100]进行分组，假设同一组中的每个数据可用该组区间的中点值代替，则得到体育成绩的折线图（如图）

（Ⅰ）体育成绩大于或等于70分的学生常被称为“体育良好”．已知该校高一年级有1000名学生，试估计高一年级中“体育良好”的学生人数；
（Ⅱ）为分析学生平时的体育活动情况，现从体育成绩在[60，70）和[80，90）的样本学生中随机抽取2人，求在抽取的2名学生中，至少有1人体育成绩在[60，70）的概率；
（Ⅲ）假设甲、乙、丙三人的体育成绩分别为a，b，c，且分别在[70，80），[80，90），[90，100]三组中，其中a，b，c∈N．当数据a，b，c的方差s²最大时，写出a，b，c的值．（结论不要求证明）
（注：s²=$\frac{1}{n}$[（x₁-$\overline{x}$）²+（x₂-$\overline{x}$）²+…+（x_n-$\overline{x}$）²]，其中$\overline{x}$为数据x₁，x₂，…，x_n的平均数）

Answer 1

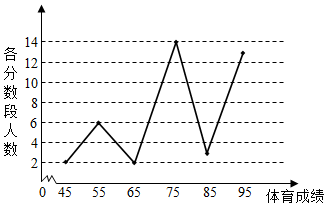
分析 （Ⅰ）由折线图知，样本中体育成绩大于或等于70分的学生有30人，由此能求出该校高一年级学生中，“体育良好”的学生人数．
（Ⅱ）设“至少有1人体育成绩在[60，70）”为事件M，记体育成绩在[60，70）的学生为A₁，A₂，体育成绩在[80，90）的学生为B₁，B₂，B₃，由此利用列举法能求出在抽取的2名学生中，至少有1人体育成绩在[60，70）的概率．
（Ⅲ）由题意，能写出数据a，b，c的方差s²最大时，a，b，c的值．

解答 解：（Ⅰ）由折线图知，样本中体育成绩大于或等于70分的学生有30人，
所以该校高一年级学生中，“体育良好”的学生人数大约为1000×$\frac{30}{40}$=750人；
（Ⅱ）设“至少有1人体育成绩在[60，70）”为事件M，
记体育成绩在[60，70）的学生为A₁，A₂，体育成绩在[80，90）的学生为B₁，B₂，B₃，
则从这两组学生中随机抽取2人，所有可能的结果如下：
（A₁，A₂），（A₁，B₁），（A₁，B₂），（A₁，B₃），（A₂，B₁），
（A₂，B₂），（A₂，B₃），（B₁，B₂），（B₁，B₃），（B₂，B₃）共10种，
而事件M所包含的结果有（A₁，A₂），（A₁，B₁），（A₁，B₂），
（A₁，B₃），（A₂，B₁），（A₂，B₂），（A₂，B₃）共7种，
因此事件M发生的概率为P（M）=$\frac{7}{10}$；
（Ⅲ）a，b，c的值分别是为70，80，100．

点评 本题考查折线图的应用，考查概率的求法，是中档题，解题时要认真审题，注意注意对立事件概率计算公式的合理运用．