
分析 (Ⅰ)利用正弦定理以及两角和与差的三角函数化简acosC+ccosA=2bcosA,结合三角形的内角和,求解A即可.
(Ⅱ)通过余弦定理以及基本不等式求出b+c的范围,再利用三角形三边的关系求出b+c的范围.
解答 (本题满分为12分)
解:(Ⅰ)在△ABC中,因为acosC+ccosA=2bcosA,
所以sinAcosC+sinCcosA=2sinBcosA,即sin(A+C)=2sinBcosA.
因为A+B+C=π,
所以sin(A+C)=sinB.
从而sinB=2sinBcosA.…(4分)
因为sinB≠0,
所以cosA=$\frac{1}{2}$.
因为0<A<π,
所以A=$\frac{π}{3}$.…(7分)
(Ⅱ)由余弦定理得,a2=b2+c2-2bccosA,
则1=b2+c2-bc,
∴(b+c)2-3bc=1,
即3bc=(b+c)2-1≤3[$\frac{1}{2}$(b+c)]2,
化简得,(b+c)2≤4(当且仅当b=c时取等号),
则b+c≤2,又b+c>a=1,
综上得,b+c的取值范围是(1,2].…(12分)
点评 本题考查正弦定理与余弦定理的应用,两角和的正弦公式,三角形的边角关系式,以及基本不等式求最值,考查分析问题、解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 2π2a3 | B. | π2a3 | C. | $\frac{{π}^{2}}{2}$a3 | D. | $\frac{{π}^{2}}{3}$a3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
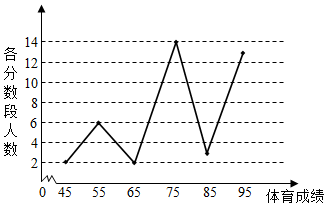
查看答案和解析>>
科目:高中数学 来源:2016-2017学年广东清远三中高一上学期月考一数学试卷(解析版) 题型:选择题
已知函数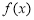 的定义域为
的定义域为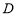 ,若对任意
,若对任意 ,当
,当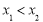 时,都有
时,都有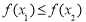 ,则称函数
,则称函数 在
在 上为非减函数.设函数
上为非减函数.设函数 在
在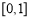 上为非减函数,且满足以下三个条件:①
上为非减函数,且满足以下三个条件:① ;②
;② ;③
;③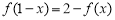 .则
.则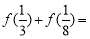 ( )
( )
A. 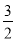 B.
B. 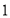 C.
C.  D.
D.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{2}$ | B. | 7 | C. | 8 | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,+∞) | B. | [$\frac{1}{10}$,10] | C. | [$\frac{1}{10}$,+∞) | D. | (0,10) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
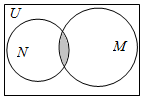 设全集U=C(复数集),i是虚数单位,集合M=Z(整数集)和N={i,i2,$\frac{1-i}{1+i}$,$\frac{(1+i)^{2}}{i}$}的关系韦恩(Venn)如图所示,则阴影部分所表示的集合是( )
设全集U=C(复数集),i是虚数单位,集合M=Z(整数集)和N={i,i2,$\frac{1-i}{1+i}$,$\frac{(1+i)^{2}}{i}$}的关系韦恩(Venn)如图所示,则阴影部分所表示的集合是( )| A. | ∅ | B. | {-1} | C. | {-1,2} | D. | {-1,1,2} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com