
分析 根据函数的奇偶性求出g(x),h(x)的表达式,然后将不等式恒成立进行参数分离,利用基本不等式进行求解即可得到结论.
解答 解:∵函数F(x)=ex满足F(x)=g(x)+h(x),且g(x),h(x)分别是R上的偶函数和奇函数,
∴ex =g(x)+h(x),e-x=g(x)-h(x),
∴g(x)=$\frac{{e}^{x}{+e}^{-x}}{2}$,h(x)=$\frac{{e}^{x}{-e}^{-x}}{2}$.
∵?x∈(0,2]使得不等式g(2x)-ah(x)≥0恒成立,即$\frac{{e}^{2x}{+e}^{-2x}}{2}$-a•$\frac{{e}^{x}{-e}^{-x}}{2}$≥0恒成立,
∴a≤$\frac{{e}^{2x}{+e}^{-2x}}{{e}^{x}{-e}^{-x}}$=$\frac{{{(e}^{x}{-e}^{-x})}^{2}+2}{{e}^{x}{-e}^{-x}}$=(ex-e-x)+$\frac{2}{{e}^{x}{+e}^{-x}}$,
设t=ex-e-x,则函数t=ex-e-x在(0,2]上单调递增,
∴0<t≤e2-e-2,
此时 不等式t+$\frac{2}{t}$≥2$\sqrt{2}$,当且仅当t=$\frac{2}{t}$,即t=$\sqrt{2}$时,取等号,∴a≤2$\sqrt{2}$,
故答案为:$({-∞,2\sqrt{2}}]$.
点评 本题主要考查函数奇偶性的应用,以及不等式恒成立问题,利用参数分离法是解决不等式恒成立问题的基本方法,本题使用了基本不等式进行求解最值,综合性较强,运算量较大,属于中档题.


 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2π2a3 | B. | π2a3 | C. | $\frac{{π}^{2}}{2}$a3 | D. | $\frac{{π}^{2}}{3}$a3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-$\frac{1}{2}$,1) | B. | (-$\frac{1}{2}$,1] | C. | (-$\frac{1}{2}$,$\frac{1}{2}$) | D. | (-$\frac{1}{2}$,$\frac{1}{2}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2016-2017学年广东清远三中高一上学期月考一数学试卷(解析版) 题型:选择题
已知函数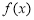 的定义域为
的定义域为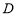 ,若对任意
,若对任意 ,当
,当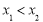 时,都有
时,都有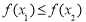 ,则称函数
,则称函数 在
在 上为非减函数.设函数
上为非减函数.设函数 在
在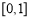 上为非减函数,且满足以下三个条件:①
上为非减函数,且满足以下三个条件:① ;②
;② ;③
;③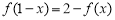 .则
.则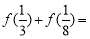 ( )
( )
A. 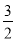 B.
B. 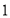 C.
C.  D.
D.
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,+∞) | B. | [$\frac{1}{10}$,10] | C. | [$\frac{1}{10}$,+∞) | D. | (0,10) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com