
| ��� | ��ʱ�� | ���� |
| һ | [0��5�� | 1 |
| �� | [5��10�� | 6 |
| �� | [10��15�� | 4 |
| �� | [15��20�� | 2 |
| �� | [20��25] | 2 |
���� ��1����ʱ������10���ӵ�������ռ�ı���Ϊ����60���Դ˱�������������
��2������6����ѡ2������һ�����ʾ����飬���оٷ��г��������п����������15�֣���ó鵽������ǡ������ͬһ����������7�֣��ɴ���ó鵽������ǡ�����Բ�ͬ��ĸ��ʣ�
��� �⣺��1����ʱ������10���ӵ�������ռ�ı���Ϊ$\frac{1+6}{15}$=$\frac{7}{15}$��
����60���˿��к�ʱ������10���ӵ�����Ϊ 60��$\frac{7}{15}$=28��
��2������е������4���˷ֱ�Ϊa1��a2��a3��a4���������2���˷ֱ�Ϊb1��b2��
����6����ѡ2������һ�����ʾ����飬
�����оٷ��г��������п����������a1��a2 ������ a1��a3 ������ a1��a4 ����
��a1��b1������ a1��b2������a2��a3������a2��a4������a2��b1������a2��b2����
��a3��a4������a3��b1������a3��b2������a4��b1������a4��b2������b1��b2��������15�֣�
�ڳ鵽������ǡ������ͬһ�飺��a1��a2 ������ a1��a3 ������ a1��a4 ������a2��a3������a2��a4������a3��a4������b1��b2��������7�֣�
�ʳ鵽������ǡ������ͬһ��ĸ���Ϊ$\frac{7}{15}$��
���� ���⿼��ŵ�������⣬�����оٳ����鷢���������¼��������������¼���Ӧ���оٷ�����������һ���ֵ�����Ҫ˼�룬���ڻ����⣮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
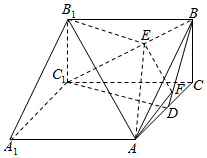 ��ͼ��������ABC-A1B1C1�У�BC��ֱ��������A1ACC1����ƽ�棬AC=2��BC=1��DΪAC�е㣬EΪ�߶�BC1�ϵ�һ�㣨�˵���⣩��ƽ��AB1E��BD���ڵ�F
��ͼ��������ABC-A1B1C1�У�BC��ֱ��������A1ACC1����ƽ�棬AC=2��BC=1��DΪAC�е㣬EΪ�߶�BC1�ϵ�һ�㣨�˵���⣩��ƽ��AB1E��BD���ڵ�F�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | {-2��-1��0} | B�� | {-2��-1��0��1} | C�� | ��-2��1�� | D�� | [-2��1] |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����

| A�� | 25 | B�� | 125 | C�� | 625 | D�� | 1350 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��һ���� | B�� | �ڶ����� | C�� | �������� | D�� | �������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | [-2��1�� | B�� | ��-1��2] | C�� | [2��3�� | D�� | [-2��3�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com