Question

14．已知某几何体的一条棱长为a，在正视图中的投影长为2$\sqrt{3}$，在侧视图，俯视图中投影长分别为m、n，且m+n=6，则a的最小值为4．

Answer 1

分析 作出线段在空间坐标系中的投影和直观图，利用勾股定理求出m，n．则a的最小值为n．

解答 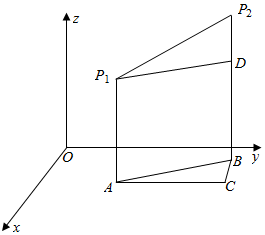解：作出空间坐标系如图，设几何体的棱为P₁P₂，作出它在平面xoy上的投影AB，
过A作AC∥y轴，过B作BC∥x轴，交点为C，则AC=2$\sqrt{3}$，BC=m，AB=n．
由勾股定理得（2$\sqrt{3}$）²+m²=n²，又∵m+n=6，∴n=4，m=2．
过P₁作P₁D⊥P₂B，则P₁D=AB=4．P₂D为P₁P₂的竖坐标之差．
∴P₁P₂=$\sqrt{{P}_{1}{D}^{2}+{P}_{2}{D}^{2}}$=$\sqrt{16+{P}_{2}{D}^{2}}$．
∴当P₂D=0时，P₁P₂取得最小值4．
故答案为：4．

点评 本题考查了物体的三视图，找到m，n的关系求出m，n是解题关键．