
分析 (Ⅰ)利用S4=5S2求出q得到通项公式,又$\left\{{\begin{array}{l}{{T_n}={n^2}{b_n}}\\{{T_{n-1}}={{(n-1)}^2}{b_{n-1}}}\end{array}}\right.$,两式作差得$\frac{b_n}{{{b_{n-1}}}}=\frac{n-1}{n+1}$然后求解{bn}的通项公式;
(Ⅱ)通过${S_n}={2^n}-1$化简${C_n}={2^n}(\frac{2}{n+1}-λ)$,利用Cn+1<Cn,求出实数λ的不等式,然后求解即可.
解答 解:(Ⅰ)∵S4=5S2即${S_2}+{S_2}{q^2}=5{S_2}$,
∴q2=4,又∵q>0,∴q=2,
∴${a_n}={2^{n-1}}$…2分
又$\left\{{\begin{array}{l}{{T_n}={n^2}{b_n}}\\{{T_{n-1}}={{(n-1)}^2}{b_{n-1}}}\end{array}}\right.$(n≥2),两式作差得$\frac{b_n}{{{b_{n-1}}}}=\frac{n-1}{n+1}$(n≥2)
得${b_n}=\frac{b_n}{{{b_{n-1}}}}•\frac{{{b_{n-1}}}}{{{b_{n-2}}}}•…•\frac{b_2}{b_1}•{b_1}=\frac{2}{n•(n+1)}$,
当n=1时也满足,故${b_n}=\frac{2}{n•(n+1)}$. …4分
(Ⅱ)∵${S_n}={2^n}-1$
∴${C_n}={2^n}(\frac{2}{n+1}-λ)$,…6分
则${C_{n+1}}-{C_n}={2^n}(\frac{4}{n+2}-\frac{2}{n+1}-λ)<0$对n∈N*都成立,
即$λ>\frac{4}{n+2}-\frac{2}{n+1}$对n∈N*都成立 …8分
而$\frac{4}{n+2}-\frac{2}{n+1}=\frac{2n}{(n+1)(n+2)}=\frac{2}{{n+\frac{2}{n}+3}}$
故当n=1或n=2时${(\frac{4}{n+2}-\frac{2}{n+1})_{max}}=\frac{1}{3}$,
∴$λ>\frac{1}{3}$…10分.
点评 本题考查数列的通项公式的求法,数列与不等式的关系,函数的最值的求法,考查计算能力.


科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{BO}=-\frac{5}{6}\overrightarrow{AB}+\frac{1}{6}\overrightarrow{AC}$ | B. | $\overrightarrow{BO}=\frac{1}{6}\overrightarrow{AB}-\frac{1}{2}\overrightarrow{AC}$ | C. | $\overrightarrow{BO}=\frac{5}{6}\overrightarrow{AB}-\frac{1}{6}\overrightarrow{AC}$ | D. | $\overrightarrow{BO}=-\frac{1}{6}\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AC}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
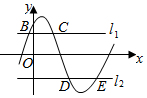 (理)如图,直线l1:y=m(0<m≤A)与函数f(x)=Acos(ωx+φ)(A>0,ω>0)的图象相交于B、C两点,直线l2:y=-m与函数f(x)=Acos(ωx+φ)(A>0,ω>0)的图象相交于D、E两点,设B(xB,yB),D(x,yD),记S(m)=|xB-xD|,则S(m)的图象大致是( )
(理)如图,直线l1:y=m(0<m≤A)与函数f(x)=Acos(ωx+φ)(A>0,ω>0)的图象相交于B、C两点,直线l2:y=-m与函数f(x)=Acos(ωx+φ)(A>0,ω>0)的图象相交于D、E两点,设B(xB,yB),D(x,yD),记S(m)=|xB-xD|,则S(m)的图象大致是( )| A. | 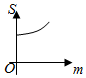 | B. | 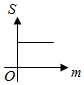 | C. | 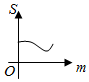 | D. |  |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com