练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    5．用平面在正方体上截下一个三棱锥，以原来正方体的那个顶点作为三棱锥的顶点，则该顶点在三棱锥的底面上的射影是这个三角形的（　　）
    A．重心B．外心C．内心D．垂心

    分析 一条侧棱就垂直于另外两条侧棱所组成的面，即垂直于在面上的底面的一条边，过顶点向底面做垂线，连接底面的顶点和垂足，根据三垂线定理得到连线是高线，得到三条高线的交点是垂心．

    解答 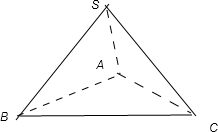解：用平面在正方体上截下一个三棱锥，以原来正方形的那个顶点作为三棱锥的顶点，
    则三棱锥的三条侧棱中，每两条之间的夹角都是90°，
    则三条侧棱两两垂直，
    即SB⊥SA，SB⊥SC，
    ∵SA∩SC=S，
    ∴SB⊥面SAC，
    ∵AC?面SAC，
    ∴SB⊥AC，
    过S向底面做垂线，垂足为O，连接BO，并延长交AC于D，
    由三垂线定理知BD⊥AC，即BD 是三角形的高线，
    ∴三棱锥的顶点在底面的射影是底面三角形的垂心，
    故选：D

    点评 本题考查棱锥的结构特征，考查逻辑思维能力和空间思维能力，是基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    15．设数列{an}满足an=3an-1+2（n≥2，n∈N+），且a1=2，bn=log3（an+1）．
    （1）证明：数列{an+1}为等比数列；
    （2）求数列{anbn}的前n项和Sn．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    16．已知椭圆C1，抛物线C2的焦点均在x轴上，从两条曲线上各取两个点，将其坐标混合记录于下表中：
    x-$\sqrt{2}$2$\sqrt{6}$9
    y$\sqrt{3}$-$\sqrt{2}$-13
    （1）求椭圆C1和抛物线C2的标准方程．
    （2）过椭圆C1右焦点F的直线l与此椭圆相交于A，B两点，若点P为直线x=4上任意一点，试证：直线PA，PF，PB的斜率成等差数列．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．如图，某大风车的半径为2m，每6s旋转一周，它的最低点O离地面0.5 m．风车圆周上一点A从最低点O开始，运动t（s）后与地面的距离为h（m），则函数h=f（t）的关系式（　　）
    A．y=-2cos$\frac{πt}{6}$+2.5B．y=-2sin$\frac{πt}{6}$+2.5C．y=-2cos$\frac{πt}{3}$+2.5D．y=-2sin$\frac{πt}{3}$+2.5

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    20．在直角坐标系xOy中，以O为极点，x正半轴为极轴建立极坐标系，曲线C1、C2的极坐标方程分别为$ρcos（θ-\frac{π}{3}）=1$，ρ=1．
    （1）写出曲线C1、C2的直角坐标方程．
    （2）判断曲线C1、C2的位置关系．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．解不等式|x-1|+|2x+1|＜2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．“五一”期间，三个家庭（每家均为一对夫妇和一个孩子）去“抚顺三块石国家森林公园”游玩，在某一景区前合影留念，要求前排站三个小孩，后排为三对夫妇，则每队夫妇均相邻，且小孩恰与自家父母排列的顺序一致的概率（　　）
    A．$\frac{1}{15}$B．$\frac{1}{90}$C．$\frac{1}{180}$D．$\frac{1}{360}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．已知$\overrightarrow{e}$和$\overrightarrow{f}$是互相垂直的单位向量，向量$\overrightarrow{{a}_{n}}$满足：$\overrightarrow{e}•\overrightarrow{{a}_{n}}$=n，$\overrightarrow{f}•\overrightarrow{{a}_{n}}$=2n，n∈N*．设θn为$\overrightarrow{{a}_{n+1}}$-$\overrightarrow{{a}_{n}}$和$\overrightarrow{{a}_{n+2}}$-$\overrightarrow{{a}_{n+1}}$的夹角，则（　　）
    A．On随着n的增大而增大B．On随着n的增大而减小
    C．随着n的增大，On先增大后减小D．随着n的增大，On先减小后增大

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．能化为普通方程x2+y-1=0的参数方程是（　　）
    A．$\left\{\begin{array}{l}x=sint\\ y={cos^2}t\end{array}\right.$B．$\left\{\begin{array}{l}x=tanφ\\ y=1-{tan^2}φ\end{array}\right.$
    C．$\left\{\begin{array}{l}x=\sqrt{1-t}\\ y=t\end{array}\right.$D．$\left\{\begin{array}{l}{x=cosθ}\\{y=si{n}^{2}θ}\end{array}\right.$

    查看答案和解析>>

    同步练习册答案