
���� ��1�����E�����꣬�����EF�е����꣬���е����깫ʽ���е�������E�������ʾ�����������߷������E�����ꣻ
��2�����ֱ��l�ķ���Ϊy=kx+1������ֱ�߷����������߷��̣���Ϊ����x��һԪ���η��̣�������������꣬���$\overrightarrow{AF}$=2$\overrightarrow{FB}$�����k��ֵ��
��3����M��s��$\frac{1}{4}{s}^{2}$����N��t��$\frac{1}{4}{t}^{2}$������OM��ON���õ�st=-16����������б�ʵõ�ֱ��MN��б��Ϊ$\frac{\frac{1}{4}��{t}^{2}-{s}^{2}��}{t-s}=\frac{1}{4}��s+t��$������õ�$y=\frac{1}{4}��s+t��x+4$���ɴ˿�˵��ֱ�߱ع���0��4���㣻
��4����PC����ֱ�߷���Ϊy-4=k��x+4������PD����ֱ�߷���Ϊy-4=-k��x+4�����ֱ�������ֱ�߷����������߷��̣����C��D���꣬��б�ʹ�ʽ�������ֱ��CD��б�ʣ�
��5����G��H����ֱ�߷���Ϊy=2x+b������ֱ�߷��̺������߷��̣����б�ʽ����0���b�ķ�Χ���ɸ���ϵ����ϵ���GH�е����꣬�õ��߶�GH�Ĵ�ֱƽ���߷��̣�ȡx=0���ɵ��߶�GH�Ĵ�ֱƽ������y���ϵĽؾ��ȡֵ��Χ��
��� ��1���⣺��x2=4y����F��0��1������E��m��0����EF�е�Ϊ��x��y����
��$\left\{\begin{array}{l}{0+m=2x}\\{1+0=2y}\end{array}\right.$����$\left\{\begin{array}{l}{x=\frac{m}{2}}\\{y=\frac{1}{2}}\end{array}\right.$������x2=4y����$\frac{{m}^{2}}{4}=4��\frac{1}{2}$����ã�m=$��2\sqrt{2}$��
��E��$��2\sqrt{2}��0$����
��2���⣺��ֱ��l��б��Ϊk����ֱ��l�ķ���Ϊy=kx+1��
����$\left\{\begin{array}{l}{y=kx+1}\\{{x}^{2}=4y}\end{array}\right.$����x2-4kx-4=0��
��A��x1��y1����B��x2��y2����
��ã�$\left\{\begin{array}{l}{{x}_{1}=2k-2\sqrt{{k}^{2}+1}}\\{{x}_{2}=2k+2\sqrt{{k}^{2}+1}}\end{array}\right.$��$\left\{\begin{array}{l}{{x}_{1}=2k+2\sqrt{{k}^{2}+1}}\\{{x}_{2}=2k-2\sqrt{{k}^{2}+1}}\end{array}\right.$��
��$\overrightarrow{AF}$=2$\overrightarrow{FB}$���ã�-x1��1-y1��=2��x2��y2-1��=��2x2��2y2-2������-x1=2x2��
��x1��x2�ֱ����-x1=2x2����ã�k=$��\frac{\sqrt{2}}{4}$��
��3��֤������M��NΪ���������������㣬����M��s��$\frac{1}{4}{s}^{2}$����N��t��$\frac{1}{4}{t}^{2}$����
��OM��ON����$st+\frac{{s}^{2}{t}^{2}}{16}=0$����st=-16��
ֱ��MN��б��Ϊ$\frac{\frac{1}{4}��{t}^{2}-{s}^{2}��}{t-s}=\frac{1}{4}��s+t��$��
��ֱ��MN���õ�бʽ����Ϊy-$\frac{1}{4}{s}^{2}=\frac{1}{4}��s+t����x-s��$������õ�$y=\frac{1}{4}��s+t��x+4$��
��ֱ�߱ع���0��4���㣻
��4���⣺��PC����ֱ�߷���Ϊy-4=k��x+4������PD����ֱ�߷���Ϊy-4=-k��x+4����
����C��x3��y3����D��x4��y4����
����$\left\{\begin{array}{l}{y=kx+4k+4}\\{{x}^{2}=4y}\end{array}\right.$���ã�x2-4kx-16k-16=0��
��x3-4=4k����x3=4k+4����${y}_{3}=4{k}^{2}+8k+4$��
ͬ�����x4=-4k+4��${y}_{4}=4{k}^{2}-8k+4$��
��${k}_{CD}=\frac{{y}_{3}-{y}_{4}}{{x}_{3}-{x}_{4}}=\frac{16k}{8k}=2$��
��5����G��H����ֱ�߷���Ϊy=2x+b��
����$\left\{\begin{array}{l}{y=2x+b}\\{{x}^{2}=4y}\end{array}\right.$����x2-8x-4b=0��
�ɡ�=��-8��2+16b��0����b��-4��
����C��x5��y5����H��x6��y6����
��x5+x6=8����G��H�е������Ϊ4��������Ϊ8+b��
���߶�GH�Ĵ�ֱƽ���߷���Ϊy-8-b=$-\frac{1}{2}$��x-4����
ȡx=0����y=10+b��
��b��-4����y��6��
���߶�GH�Ĵ�ֱƽ������y���ϵĽؾ��ȡֵ��Χ�ǣ�6��+�ޣ���
���� ������Ҫ�����������ߵ�Ӧ�ã�ƽ�����ʽ�Ļ���֪ʶ�������˿����Ļ���֪ʶ���ۺ����ú�֪ʶǨ�Ƶ����������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ֱ������ABC-A1B1C1�У�AB=BC=2����ABC=120�㣬DΪAC���е㣬PΪ��A1B�ϵĶ��㣮
��ͼ����ֱ������ABC-A1B1C1�У�AB=BC=2����ABC=120�㣬DΪAC���е㣬PΪ��A1B�ϵĶ��㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
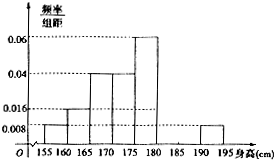 ��ijУ��800�������������ȡ50�˲������ߣ�����ѧ�����߽��ڽ���155cm��195cm֮�䣬��������������·�ʽ�ֳɰ��飺��һ��[155��160�����ڶ���[160��165������..���ڰ���[190��195]����ͼ�ǰ��������鷽���õ���Ƶ�ʷֲ�ֱ��ͼ��һ���֣���֪��һ����ڰ���������ͬ�������������Ϊ4�ˣ�
��ijУ��800�������������ȡ50�˲������ߣ�����ѧ�����߽��ڽ���155cm��195cm֮�䣬��������������·�ʽ�ֳɰ��飺��һ��[155��160�����ڶ���[160��165������..���ڰ���[190��195]����ͼ�ǰ��������鷽���õ���Ƶ�ʷֲ�ֱ��ͼ��һ���֣���֪��һ����ڰ���������ͬ�������������Ϊ4�ˣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ֱ֪������ABC-A��B��C�������BAC=90�㣬AB=AC=$\frac{1}{2}$AA��=2����M��N�ֱ�ΪA��B��B��C����е㣮
��ֱ֪������ABC-A��B��C�������BAC=90�㣬AB=AC=$\frac{1}{2}$AA��=2����M��N�ֱ�ΪA��B��B��C����е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ���������ȼ� | �� | �� | �����Ⱦ | �ж���Ⱦ | �ض���Ⱦ | ������Ⱦ |
| AQIֵ��Χ | [0��50�� | [50��100�� | [100��150�� | [150��200�� | [200��300�� | 300������ |
| �������� | AQI��ֵ | �������� | AQI��ֵ |
| ���� | 108 | ���� | 104 |
| ���� | 92 | ���� | 42 |
| �������� | 37 | �Ϻ� | x |
| ������˹ | 56 | ���� | 114 |
| ������ | 61 | ��� | 105 |
| ����� | 456 | ʯ��ׯ | 93 |
| AQIƽ��ֵ��135 | AQIƽ��ֵ��90 | ||
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com