
分析 由y=x-sinx(0≤x≤2π),求出导数,判断单调性可得0≤x-sinx≤2π,而e0-eπ+π<0,即可得到所求范围.
解答 解:e0-eπ≤θ-sinθ-π,
即为1+π-eπ≤θ-sinθ,
可令y=x-sinx(0≤x≤2π),
y′=1-cosx≥0,即函数y=x-sinx在[0,2π]递增,
可得0≤x-sinx≤2π,即0≤θ-sinθ≤2π,
而e0-eπ+π<0,
即有e0-eπ≤θ-sinθ-π在[0,2π]恒成立,
则θ的取值范围是[0,2π],
故答案为:[0,2π].
点评 本题考查不等式的解法,注意运用函数的单调性,结合不等式的性质,考查运算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | (1,$\sqrt{3}$] | B. | [$\frac{\sqrt{3}}{3}$,1) | C. | ($\frac{\sqrt{3}}{3}$,1) | D. | [$\frac{\sqrt{3}}{3}$,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
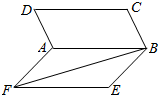 如图,四边形ABCD与四边形ABEF都是正方形,且二面角D-AB-F的大小为60°,则异面直线AD与BF所成角的余弦值是$\frac{\sqrt{2}}{4}$.
如图,四边形ABCD与四边形ABEF都是正方形,且二面角D-AB-F的大小为60°,则异面直线AD与BF所成角的余弦值是$\frac{\sqrt{2}}{4}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com