
分析 (1)化简函数,利用三角形MNH的面积为$\frac{\sqrt{2}π}{4}$,求ω的值,可得函数f(x)的单调递增区间;
(2)锐角三角形ABC,边c=2,所对角C满足f(C)=1,S=$\frac{1}{2}absinC$=2$\sqrt{2}$sinAsinB=$\sqrt{2}$cos(A-B)+1=$\sqrt{2}$cos(2A-135°),即可求其面积S的取值范围.
解答 解:(1)f(x)=sin4ωx-cos4ωx+2sinωxcosωx=sin2ωx-cos2ωx=$\sqrt{2}$sin(2ωx-$\frac{π}{4}$),
∵三角形MNH的面积为$\frac{\sqrt{2}π}{4}$,
∴$\frac{1}{2}×\frac{π}{2ω}×\sqrt{2}$=$\frac{\sqrt{2}π}{4}$,
∴ω=1,
∴f(x)=$\sqrt{2}$sin(2x-$\frac{π}{4}$),
由2kπ-$\frac{π}{2}$≤2x-$\frac{π}{4}$≤2kπ+$\frac{π}{2}$,得函数f(x)的单调递增区间为[kπ-$\frac{π}{8}$,kπ+$\frac{3π}{8}$](k∈Z);
(2)由题意,sin(2C-$\frac{π}{4}$)=$\frac{\sqrt{2}}{2}$,三角形ABC是锐角三角形,
∴2C-$\frac{π}{4}$=$\frac{π}{4}$,∴C=$\frac{π}{4}$,
由正弦定理可得2R=$\frac{c}{sinC}$=2$\sqrt{2}$,
S=$\frac{1}{2}absinC$=2$\sqrt{2}$sinAsinB=$\sqrt{2}$cos(A-B)+1=$\sqrt{2}$cos(2A-135°),
∵0°<A<90°,0°<135°-A<90°,
∴45°<A<90°,
∴-45°<2A-135°<45°,
∴1<S≤$\sqrt{2}$.
点评 本题考查三角函数的化简,考查三角函数的图形与性质,考查学生的计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | 2 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
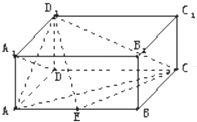 如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AD上移动.
如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AD上移动.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
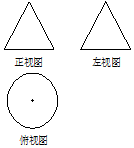 如图,一个空间几何体正视图与左视图为全等的等边三角形,俯视图为一个半径为1的圆及其圆心,那么这个几何体的表面积为( )
如图,一个空间几何体正视图与左视图为全等的等边三角形,俯视图为一个半径为1的圆及其圆心,那么这个几何体的表面积为( )| A. | π | B. | 3π | C. | 2π | D. | $π+\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com