
分析 分别由命题命题p和命题q解出它们对变的不等式的解集,根据p是q的必要不充分条件,说明q的解集是p解集的真子集,建立不等式组可得出实数m的取值范围.
解答 解:命题p:(x-m)(x-m-2)≤0⇒m≤x≤m+2,
命题q:|4x-3|≤1⇒-1≤4x-3≤1⇒$\frac{1}{2}$≤x≤1,
∵p是q的必要非充分条件
∴[$\frac{1}{2}$,1]⊆[m,m+2]
∴$\left\{\begin{array}{l}{m≤\frac{1}{2}}\\{m+2≥1}\end{array}\right.$(等号不能同时成立)⇒-1≤m≤$\frac{1}{2}$
故答案为:$[-1,\frac{1}{2}]$.
点评 本题以不等式的解集为例,考查了充分条件与必要条件的判断,属于基础题.解题时注意充分条件与必要条件之间范围的包含关系.


 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,有一直角墙角,两边的长度足够长,若P处有一棵树与两墙的距离分别是4m和am(0<a<12),不考虑树的粗细.现用16m长的篱笆,借助墙角围成一个矩形花圃ABCD.设此矩形花圃的最大面积为u,若将这棵树围在矩形花圃内,则函数u=f(a)(单位m2)的图象大致是( )
如图,有一直角墙角,两边的长度足够长,若P处有一棵树与两墙的距离分别是4m和am(0<a<12),不考虑树的粗细.现用16m长的篱笆,借助墙角围成一个矩形花圃ABCD.设此矩形花圃的最大面积为u,若将这棵树围在矩形花圃内,则函数u=f(a)(单位m2)的图象大致是( )| A. |  | B. | 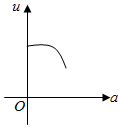 | C. | 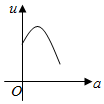 | D. | 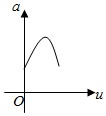 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | i | C. | 1 | D. | -i |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 60° | B. | 90° | C. | 120° | D. | 150° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com