
| A. | 1 | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{5}$ |
分析 作差g(t)-f(t)=2t+m+1,从而可知t≥-$\frac{m+1}{2}$时g(t)≥f(t),从而化为g(t)=t2+(m+2)t+n2+m+1在t≥-$\frac{m+1}{2}$时g(t)min=(-$\frac{m+1}{2}$+$\frac{m+2}{2}$)2+n2+m+1-$\frac{(m+2)^{2}}{4}$≥0恒成立,从而可得|m|≤1;从而结合选项解得.
解答 解:∵g(t)-f(t)=t2+(m+2)t+n2+m+1-(t2+mt+n2)=2t+m+1,
∴当2t+m+1≥0,即t≥-$\frac{m+1}{2}$时,g(t)≥f(t),
而g(t)=t2+(m+2)t+n2+m+1=(t+$\frac{m+2}{2}$)2+n2+m+1-$\frac{(m+2)^{2}}{4}$,
∵-$\frac{m+1}{2}$>-$\frac{m+2}{2}$,
∴g(t)min=(-$\frac{m+1}{2}$+$\frac{m+2}{2}$)2+n2+m+1-$\frac{(m+2)^{2}}{4}$≥0恒成立,
即m2≤1+4n2恒成立,
故|m|≤1;
结合选项可知,A正确;
故选:A.
点评 本题考查了分类讨论的思想应用及作差法的应用,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | f(x0)<x0 | B. | f(x0)=x0 | C. | f(x0)>x0 | D. | f(x0)=-x0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{6}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
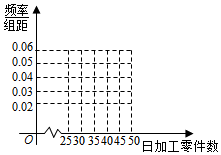 随机观测生产某种们零件的某工厂20名工人的日加工零件数(单位:件),获得数据如下:30,42,41,36,44,48,37,25,45,43,31,49,34,33,43,38,32,46,39,36.根据上述数据得到样本的频率分布表如下:
随机观测生产某种们零件的某工厂20名工人的日加工零件数(单位:件),获得数据如下:30,42,41,36,44,48,37,25,45,43,31,49,34,33,43,38,32,46,39,36.根据上述数据得到样本的频率分布表如下:| 分组 | 频数 | 频率 |
| [25,30] | 2 | 0.10 |
| (30,35] | 4 | 0.20 |
| (35,40] | 5 | 0.25 |
| (40,45] | m | fm |
| (45,50] | n | fn |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (7,$\frac{29}{4}$) | B. | (21,$\frac{135}{4}$) | C. | [27,30) | D. | (27,$\frac{135}{4}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 函数f(x)=sinxcosx的最小正周期为π | |
| B. | 函数$f(x)=lnx+\frac{1}{2}x-2$在区间(2,3)内有零点 | |
| C. | 已知函数$f(x)={log_a}({x^2}-2x+2)$,若$f(\frac{1}{2})>0$,则0<a<1 | |
| D. | 在某项测量中,测量结果ξ服从正态分布N(2,σ2)(σ>0).若ξ在(-∞,1)内取值的概率为0.1,则ξ在(2,3)内取值的概率为0.4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com