
分析 由最大值以及风轮的直径求出a和c,由周期求出ω,由最低点求出b的值.
解答 解:∵风叶轮离地面的高度y与时间t的关系函数y=asin[ω(t-b)]+c,
由题意可得周期T=$\frac{2π}{ω}$=$\frac{1}{2}$分钟=30(s),∴ω=$\frac{π}{15}$.
由题意可得振幅a=7,c=7.5.
再根据当t=0时,y取得最小值为0.5,可得7sin[$\frac{π}{15}$•(-b)]=-7,
∴$\frac{-bπ}{15}$=-$\frac{π}{2}$,即 b=$\frac{15}{2}$,
点评 本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,由函数的图象的顶点坐标求出A,由周期求出ω,由特殊点的坐标求出φ的值,属于基础题.


 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
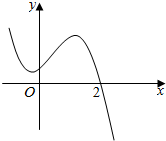
| A. | (-∞,1] | B. | [1,+∞) | C. | [0,+∞) | D. | (-∞,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=log${\;}_{\frac{1}{2}}$x | B. | y=2x-1 | C. | $y={x^2}-\frac{1}{2}$ | D. | y=-x3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{3}$ | B. | -$\frac{2}{3}$ | C. | $\frac{3}{2}$ | D. | -$\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{4}{5}$ | B. | -$\frac{3}{5}$ | C. | $\frac{4}{3}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
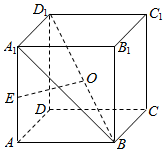 如图,在正方体ABCD-A1B1C1D1中,AA1=2,E为AA1的中点,O是BD1的中点.
如图,在正方体ABCD-A1B1C1D1中,AA1=2,E为AA1的中点,O是BD1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 6 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com