
分析 此题要求方程的解集,主要还是化简方程左边的行列式得一元二次方程求出x即可.
解答 解:因为f(x)=$|\begin{array}{l}{1}&{1}&{1}\\{x}&{-1}&{1}\\{{x}^{2}}&{2}&{1}\end{array}|$得到方程f(x)=0,
即$|\begin{array}{l}{1}&{1}&{1}\\{x}&{-1}&{1}\\{{x}^{2}}&{2}&{1}\end{array}|$=0
化简得:1×(-1)×1+1×1×x2+x×1×1-x2×(-1)×1-x×1×1-1×1×1=0
化简得:x2=1
解得:x1=1,x2=-1.
故答案为:{-1,1}.
点评 此题考查学生化简行列式的能力,解方程的能力


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{5}$ | B. | $2\sqrt{5}$ | C. | $3\sqrt{5}$ | D. | $4\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1)(3) | B. | (2)(3) | C. | (1)(4) | D. | (2)(4) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
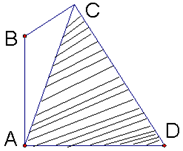 在路边安装路灯,灯柱AB与地面垂直,灯杆BC与灯柱AB所在平面与路面垂直,且∠ABC=120°,路灯采用锥形灯罩,射出的光线如图中的阴影部分所示,∠ACD=60°,AD=24米,∠ACB=θ(30°≤θ≤45°).
在路边安装路灯,灯柱AB与地面垂直,灯杆BC与灯柱AB所在平面与路面垂直,且∠ABC=120°,路灯采用锥形灯罩,射出的光线如图中的阴影部分所示,∠ACD=60°,AD=24米,∠ACB=θ(30°≤θ≤45°).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x<-1或x>1} | B. | {x|x<-2或x>2} | C. | {x|-1<x<1} | D. | {x|-2<x<2} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com