
分析 (1)求出f(x)的导数,可得在点(e,1)处的切线的斜率,由题意可得f(e)=1,由a=1,可得b,c,再由g(x)=f(x)-lnx=x2-2e2lnx+e2,求出导数,判断单调性,即可得证;
(2)由题意可得f(1)≤k+m≤f(1),即有f(1)=k+m,即为k+m=a+c,由条件可得kx2+(m-k)x-m≥0,可得k>0,且(m-k)2+4km≤0,求得k+m=0,再由lnx≤x-1≤xlnx,即可得到k=1,m=-1.
解答 解:(1)证明:函数f(x)=ax2+blnx+c的导数为f′(x)=2ax+$\frac{b}{x}$,
可得在点(e,1)处的切线的斜率为2ae+$\frac{b}{e}$,
由题意可得f(e)=1,即ae2+b+c=1,
又2ae+$\frac{b}{e}$=$\frac{1}{e}$,a=1,
解得b=1-2e2,c=e2,
g(x)=f(x)-lnx=x2-2e2lnx+e2,
g′(x)=2x-2e2•$\frac{1}{x}$,
当x>e时,g′(x)>0,g(x)递增;
当0<x<e时,g′(x)<0,g(x)递减.
即有x=e处g(x)取得最小值,且为0,
可得g(x)≥0,即有f(x)-lnx≥0,
则原不等式成立;
(2)由题意可得f(1)≤k+m≤f(1),
即有f(1)=k+m,即为k+m=a+c,
由(1)可得,k+m=a+ae2,
又f(x)≤kx+m
且f(x)≥k+$\frac{m}{x}$,
即为kx+m≥k+$\frac{m}{x}$,即有kx2+(m-k)x-m≥0,
可得k>0,且(m-k)2+4km≤0,即(m+k)2≤0,
可得m+k=0,
解得a=0,b=1-2ae2=1,c=ae2=0,
则f(x)=lnx,
由lnx≤kx+m≤xlnx恒成立,可得
lnx≤k(x-1)≤xlnx恒成立,
由lnx-(x-1)的导数为$\frac{1}{x}$-1,
当x>1时,lnx-(x-1)递减,0<x<1时,lnx-(x-1)递增,
可得lnx-(x-1)≤0,即lnx≤x-1;
又xlnx-(x-1)的导数为1+lnx-1=lnx,
当x>1时,xlnx-(x-1)递增,0<x<1时,xlnx-(x-1)递减,
可得xlnx-(x-1)≥0,即有xlnx≥x-1,
故lnx≤x-1≤xlnx.
可得k=1,m=-1.
点评 本题考查导数的运用:求切线的斜率和单调区间、极值和最值,考查不等式的证明,注意运用特殊值法和构造函数,运用单调性,考查化简整理的运算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
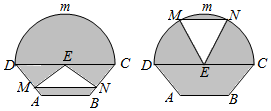 如图所示的是自动通风设施.该设施的下部ABCD是等腰梯形,其中AB=1米,高0.5米,CD=2米.上部CmD是个半圆,固定点E为CD的中点.△EMN是由电脑控制其形状变化的三角通风窗(阴影部分均不通风),MN是可以沿设施边框上下滑动且始终保持和CD平行的伸缩横杆.
如图所示的是自动通风设施.该设施的下部ABCD是等腰梯形,其中AB=1米,高0.5米,CD=2米.上部CmD是个半圆,固定点E为CD的中点.△EMN是由电脑控制其形状变化的三角通风窗(阴影部分均不通风),MN是可以沿设施边框上下滑动且始终保持和CD平行的伸缩横杆.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | b<c<a | B. | a<b<c | C. | c<a<b | D. | b<a<c |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com