
分析 f(x)=(x-$\frac{1}{2}$)(x+$\frac{1}{3}$)(x+$\frac{1}{2}$)(x+1)(x+2)所有子集的“乘积”之和即f(x)展开式中所有项的系数之和T-1.
解答 解:f(x)=(x-$\frac{1}{2}$)(x+$\frac{1}{3}$)(x+$\frac{1}{2}$)(x+1)(x+2)所有子集的“乘积”之和即f(x)展开式中所有项的系数之和T-1,
令x=1,则T=$\frac{1}{2}$×$\frac{4}{3}$×$\frac{3}{2}$×2×3=6,
∴T-1=5,
故答案为:5
点评 本题考查的知识点是元素与集合关系的判定,函数展开式的系数问题,转化困难,属于难题.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:选择题
| A. | f($-\frac{π}{2}$)<f($\sqrt{2}$)<f(e) | B. | f(e)<f($-\frac{π}{2}$)<f($\sqrt{2}$) | C. | f(e)<f($\sqrt{2}$)<f($-\frac{π}{2}$) | D. | f($\sqrt{2}$)<f($-\frac{π}{2}$)<f(e) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
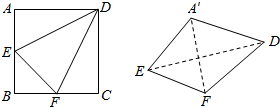 如图,边长为2的正方形ABCD中,点E、F分别 是AB、BC的中点,将△ADE,△EBF,△FCD分别沿DE,EF,FD折起,使得A、B、C三点重合于点A′,若四面体A′EFD的四个顶点在同一个球面上,则该球的表面积为( )
如图,边长为2的正方形ABCD中,点E、F分别 是AB、BC的中点,将△ADE,△EBF,△FCD分别沿DE,EF,FD折起,使得A、B、C三点重合于点A′,若四面体A′EFD的四个顶点在同一个球面上,则该球的表面积为( )| A. | 8π | B. | 6π | C. | 11π | D. | 5π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 等边三角形 | B. | 锐角三角形 | C. | 直角三角形 | D. | 钝角三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①③ | B. | ②③ | C. | ③④ | D. | ②④ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com