
分析 若不等式xy≤ax2+2y2恒成立,则a≥-2($\frac{y}{x}$)2+$\frac{y}{x}$恒成立,令t=$\frac{y}{x}$,结合二次函数的图象和性质,求得函数的最值,可得答案.
解答 解:若不等式xy≤ax2+2y2恒成立,
则a≥-2($\frac{y}{x}$)2+$\frac{y}{x}$恒成立,
令t=$\frac{y}{x}$,x∈[2,4],y∈[2,3],则t∈[$\frac{1}{2}$,$\frac{3}{2}$],
则u=-2($\frac{y}{x}$)2+$\frac{y}{x}$=-2t2+t在[$\frac{1}{2}$,$\frac{3}{2}$]上为减函数,
当t=$\frac{1}{2}$时,u取最大值0,
故a≥0,
故答案为:a≥0
点评 本题考查的知识点是恒成立问题,二次函数的图象和性质,函数的最值及其几何意义,难度中档.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
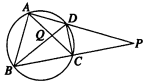 如图所示,圆内接四边形ABCD的一组对边AD,BC的延长线相交于点P,对角线AC,BD相交于点Q,则图中相似三角形共有( )
如图所示,圆内接四边形ABCD的一组对边AD,BC的延长线相交于点P,对角线AC,BD相交于点Q,则图中相似三角形共有( )| A. | 4对 | B. | 2对 | C. | 5对 | D. | 3对 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $y=-{x^{\frac{1}{2}}}$ | B. | y=-x2+|x| | C. | y=ln|x| | D. | y=-x2+x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com