
分析 由$\sqrt{8x-{x}^{2}}$-x-m=0得$\sqrt{8x-{x}^{2}}$=x+m,设y=$\sqrt{8x-{x}^{2}}$和y=x+m,利用数形结合进行求解即可.
解答 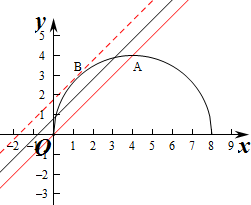 解:由$\sqrt{8x-{x}^{2}}$-x-m=0得$\sqrt{8x-{x}^{2}}$=x+m,设y=$\sqrt{8x-{x}^{2}}$和y=x+m,
解:由$\sqrt{8x-{x}^{2}}$-x-m=0得$\sqrt{8x-{x}^{2}}$=x+m,设y=$\sqrt{8x-{x}^{2}}$和y=x+m,
则8x-x2=y2,
即(x-4)2+y2=16,(y≥0),
作出对应的图象如图:
当直线y=x+m经过点O时,m=0,此时直线和半圆有两个交点,
当直线y=x+m与半圆相切时,(m>0),
圆心(4,0)到直线的距离d=$\frac{|4+m|}{\sqrt{2}}$=4,
即|m+4|=4$\sqrt{2}$,
解得m=4$\sqrt{2}$-4,或m=-4$\sqrt{2}$-4,(舍),
故方程$\sqrt{8x-{x}^{2}}$-x-m=0有两个不等的实数解,
则0≤m<4$\sqrt{2}$-4,
故答案为:0≤m<4$\sqrt{2}$-4
点评 本题主要考查函数和方程的应用,利用条件转化为两个函数之间的关系,利用数形结合是解决本题的关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (x-1)2+y2=5 | B. | (x-1)2+y2=$\frac{9}{2}$ | C. | (x-$\frac{1}{2}$)2+(y-$\frac{1}{2}$)2=5 | D. | (x-$\frac{1}{2}$)2+(y-$\frac{1}{2}$)2=$\frac{9}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
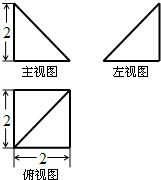 如图为一个几何体的三视图,其主、左视图均为等腰直角三角形,俯视图的外轮廓是正方形(尺寸如图),则该几何体的外接球的表面积为( )
如图为一个几何体的三视图,其主、左视图均为等腰直角三角形,俯视图的外轮廓是正方形(尺寸如图),则该几何体的外接球的表面积为( )| A. | 4π | B. | 8π | C. | 12π | D. | 16π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{9}$ | B. | -$\frac{7}{9}$ | C. | $\frac{8}{9}$ | D. | -$\frac{8}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 1 | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com