
(9分)
已知圆C: 内有一点P(2,2),过点P作直线l交圆C于A、B两点.
内有一点P(2,2),过点P作直线l交圆C于A、B两点.
(1)当l经过圆心C时,求直线l的方程;
(2)当弦AB被点P平分时,写出直线l的方程;
(3)当直线l的倾斜角为45º时,求弦AB的长.
(1)已知圆C: 的圆心为C(1,0),因直线过点P、C,所以直线l的斜率为2, 直线l的方程为y=2(x-1),即 2x-y-2="0. " ----
的圆心为C(1,0),因直线过点P、C,所以直线l的斜率为2, 直线l的方程为y=2(x-1),即 2x-y-2="0. " ---- ---------------3分
---------------3分
(2) 当弦AB被点P平分时,l⊥PC, 直线l的方程为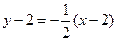 , 即 x+2y-6=0
, 即 x+2y-6=0
------------------6分
(3)当直线l的倾斜角为45º时,斜率为1,直线l的方程为y-2="x-2" ,即 x-y="0 "
圆心C到直线l的距离为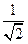 ,圆的半径为3, --------------------------8分
,圆的半径为3, --------------------------8分
弦AB的长为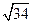 . ----------
. ---------- -----------------------9分
-----------------------9分
解析


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:解答题
直线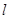 过点
过点 且斜率为
且斜率为 >
> ,将直线
,将直线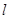 绕
绕 点按逆时针方向旋转45°得直线
点按逆时针方向旋转45°得直线 ,若直线
,若直线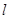 和
和 分别与
分别与 轴交于
轴交于 ,
, 两点.(1)用
两点.(1)用 表示直线
表示直线 的斜率;(2)当
的斜率;(2)当 为何值时,
为何值时, 的面积最小?并求出面积最小时直线
的面积最小?并求出面积最小时直线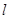 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
16.(本小题满分8分)直线l过直线x + y-2 = 0和直线x-y + 4 = 0的交点,且与直线3x-2y + 4 = 0平行,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知三角形ABC的顶点坐标为A(-1,5)、B(-2,-1)、C(4,3),M是BC边上的中点.
(Ⅰ)求AB边所在的直线方程;
(Ⅱ)求中线AM的长.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分14分)
已知点 是⊙
是⊙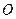 :
: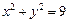 上的任意一点,过
上的任意一点,过 作
作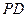 垂直
垂直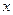 轴于
轴于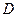 ,动点
,动点 满足
满足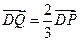 。
。
(1)求动点 的轨迹方程;
的轨迹方程;
(2)已知点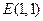 ,在动点
,在动点 的轨迹上是否存在两个不重合的两点
的轨迹上是否存在两个不重合的两点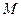 、
、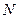 ,使
,使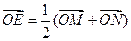 (O是坐标原点),若存在,求出直线
(O是坐标原点),若存在,求出直线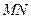 的方程,若不存在,请说明理由。
的方程,若不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分12分)已知O(0,0)、A(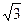 ,0)为平面内两定点,动点P满足|PO|+|PA|=2.
,0)为平面内两定点,动点P满足|PO|+|PA|=2.
(I)求动点P的轨迹方程;
(II)设直线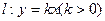 与(I)中点P的轨迹交于B、C两点.求△ABC的最大面积及此时
与(I)中点P的轨迹交于B、C两点.求△ABC的最大面积及此时
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com