
| A. | $\frac{x^2}{8}-\frac{y^2}{10}=1$ | B. | $\frac{x^2}{5}-\frac{y^2}{4}=1$ | C. | $\frac{x^2}{4}-\frac{y^2}{5}=1$ | D. | $\frac{x^2}{4}-\frac{y^2}{3}=1$ |
分析 求出双曲线的渐近线方程可得$\frac{b}{a}$=$\frac{\sqrt{5}}{2}$,①求出椭圆的焦点坐标,可得c=3,即a2+b2=9,②,解方程可得a,b的值,进而得到双曲线的方程.
解答 解:双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的一条渐近线方程为y=$\frac{{\sqrt{5}}}{2}$x,
可得$\frac{b}{a}$=$\frac{\sqrt{5}}{2}$,①
椭圆$\frac{x^2}{12}+\frac{y^2}{3}$=1的焦点为(±3,0),
可得c=3,即a2+b2=9,②
由①②可得a=2,b=$\sqrt{5}$,
则双曲线的方程为$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{5}$=1.
故选:C.
点评 本题考查双曲线的方程的求法,注意运用双曲线的渐近线方程和椭圆的焦点,考查运算能力,属于基础题.


 走进文言文系列答案
走进文言文系列答案科目:高中数学 来源: 题型:选择题
| A. | c<b<a | B. | a<c<b | C. | b<a<c | D. | c<a<b |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,△AOB为等腰直角三角形,OA=l,OC为斜边AB的髙,点P在射线OC 上,则$\overrightarrow{AP}$•$\overrightarrow{OP}$的最小值为( )
如图,△AOB为等腰直角三角形,OA=l,OC为斜边AB的髙,点P在射线OC 上,则$\overrightarrow{AP}$•$\overrightarrow{OP}$的最小值为( )| A. | -1 | B. | -$\frac{1}{4}$ | C. | -$\frac{1}{8}$ | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
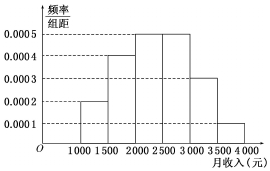 某市统计局就本地居民的月收入调查了10000人,并根据所得数据画了样本的频率分布直方图(每个分组包括左端点,不包括右端点,如第一组表示月收入在[1000,1500)(单位:元)).
某市统计局就本地居民的月收入调查了10000人,并根据所得数据画了样本的频率分布直方图(每个分组包括左端点,不包括右端点,如第一组表示月收入在[1000,1500)(单位:元)).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | $-\frac{4}{3}$ | C. | $-\frac{3}{2}$ | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在三棱柱ABC-A1B1C1中,AB⊥BC,顶点A1在底面ABC内的射影恰好是AB的中点O,且AB=BC=2.OA1=2,
如图,在三棱柱ABC-A1B1C1中,AB⊥BC,顶点A1在底面ABC内的射影恰好是AB的中点O,且AB=BC=2.OA1=2,查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{6}$ | D. | $\frac{3}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-kπ-$\frac{π}{12}$,-kπ+$\frac{5π}{12}$],k∈Z | B. | [2kπ-$\frac{π}{6}$,2kπ+$\frac{5π}{6}$],k∈Z | ||
| C. | [kπ+$\frac{5π}{12}$,kπ+$\frac{11π}{12}$],k∈Z | D. | [kπ-$\frac{π}{6}$,kπ+$\frac{π}{3}$],k∈Z |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com