
分析 (1)利用指数运算性质即可得出;
(2)利用对数的运算法则即可得出.
解答 解:(1)原式=$(\frac{3}{2})^{2×\frac{1}{2}}$-1-$(\frac{2}{3})^{-3×(-\frac{2}{3})}$+$(\frac{2}{3})^{-1×(-2)}$
=$\frac{3}{2}$-1-$\frac{4}{9}$+$\frac{4}{9}$
=$\frac{1}{2}$.
(2)原式=2-2+$\frac{3}{2}$+log24
=$\frac{3}{2}$+2
=$\frac{7}{2}$.
点评 本题考查了对数与指数的运算法则,考查了推理能力与计算能力,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | 2$\sqrt{5}$ | C. | 2 | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
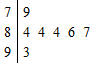 我校为了丰富同学们的课余生活,特举办了一次挑战主持人大赛,如图是七位评委为某选手打出的分数的茎叶图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )
我校为了丰富同学们的课余生活,特举办了一次挑战主持人大赛,如图是七位评委为某选手打出的分数的茎叶图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )| A. | 4;4 | B. | 5;1.6 | C. | 84;4 | D. | 85;1.6 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com