
分析 利用空间线线、线面、面面的位置关系,对①②③④逐个分析即可得到答案.
解答 解:对于①,$\left.\begin{array}{l}{n∥α}\\{m?α}\end{array}\right\}$⇒m∥n或m与n异面,故①错误;
对于②,$\left.\begin{array}{l}{n∥m}\\{m?β}\end{array}\right\}$⇒n∥β或n?β,故②错误;
对于③,$\left.\begin{array}{l}{m?α}\\{n?β}\end{array}\right\}$⇒m,n可能平行或相交,也可能异面,故③错误;
对于④,$\left.\begin{array}{l}{n∥β}\\{m∥α}\end{array}\right\}$⇒m∥n或m、n相交或异面,故④错误.
综上所述,所有假命题的序号为①②③④,
故答案为:①②③④.
点评 本题考查命题的真假判断与应用,考查空间线线、线面、面面的位置关系,考查空间想象能力,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | 在△ABC中,a:b:c=sinA:sinB:sinC | |
| B. | 在△ABC中,若sin2A=sin2B,则a=b | |
| C. | 在△ABC中,若sinA>sinB,则A>B,若A>B,则sinA>sinB | |
| D. | 在△ABC中,$\frac{a}{sinA}=\frac{b+c}{sinB+sinC}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
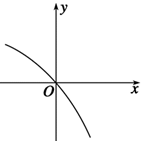 已知函数f(x)的定义域为R,f′(x)为f(x)的导函数,函数y=f′(x)的图象如图所示,且f(-2)=1,f(3)=1,则不等式f(x-3)>1的解集为( )
已知函数f(x)的定义域为R,f′(x)为f(x)的导函数,函数y=f′(x)的图象如图所示,且f(-2)=1,f(3)=1,则不等式f(x-3)>1的解集为( )| A. | (1,6) | B. | (-1,5) | C. | (0,5) | D. | (3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | eπ+1>π•ee | B. | 3eπ<πe3 | C. | 3e2>2e3 | D. | e${\;}^{\sqrt{2}}$<$\sqrt{2}$e |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com