
分析 (Ⅰ)求出函数的导数,解关于导函数的不等式,求出函数的单调区间即可;
(Ⅱ)由已知得f(x)的定义域为(0,1)∪(1,+∞),f′(x)=-a+$\frac{lnx-1}{{(lnx)}^{2}}$在(1,+∞)上恒成立,由此利用导数性质能求出a的最大值;
(Ⅲ)通过分析,问题等价于:“当x∈[e,e2]时,有gmax(x)≤$\frac{1}{4}$”,结合(Ⅱ)及g′(x),分①a≥$\frac{1}{4}$、②a≤0、③0<a<$\frac{1}{4}$三种情况讨论即可.
解答 解:(Ⅰ)a=1时,f(x))=x-xlnx,f′(x)=-lnx,
令f′(x)>0,解得:0<x<1,令f′(x)<0,解得:x>1,
∴f(x)在(0,1)递增,在(1,+∞)递减;
(Ⅱ)由已知得g(x)=$\frac{x}{lnx}$-ax,函数的定义域为(0,1)∪(1,+∞),
∵g(x)在(1,+∞)上为减函数,
∴g′(x)=-a+$\frac{lnx-1}{{(lnx)}^{2}}$≤0在(1,+∞)上恒成立,
-a≤$\frac{1}{{(lnx)}^{2}}$-$\frac{1}{lnx}$=($\frac{1}{lnx}$-$\frac{1}{2}$)2-$\frac{1}{4}$,
令h(x)=($\frac{1}{lnx}$-$\frac{1}{2}$)2-$\frac{1}{4}$,
故当$\frac{1}{lnx}$=$\frac{1}{2}$,即x=e2时,
h(x)的最小值为-$\frac{1}{4}$,∴-a≤-$\frac{1}{4}$,
即a≥$\frac{1}{4}$;最小值为$\frac{1}{4}$;
(Ⅲ)若$?{x_0}∈[{e,{e^2}}]$,使得$f({x_0})≤\frac{1}{4}ln{x_0}$成立,结合(Ⅱ)得:
问题等价于:“当x∈[e,e2]时,有gmax(x)≤$\frac{1}{4}$”,
∵g′(x)=-a+$\frac{lnx-1}{{(lnx)}^{2}}$,由(Ⅱ)知 $\frac{lnx-1}{{(lnx)}^{2}}$∈[0,$\frac{1}{4}$],
①当a≥$\frac{1}{4}$时,g′(x)≤0在[e,e2]上恒成立,因此f(x)在[e,e2]上为减函数,
则fmax(x)=g(e)=e-ae≤$\frac{1}{4}$,故a≥1-$\frac{1}{4e}$;
②当a≤0时,g′(x)≥0在[e,e2]上恒成立,因此g(x)在[e,e2]上为增函数,
则gmax(x)=g(e2)=-ae2+$\frac{{e}^{2}}{2}$≤$\frac{1}{4}$,解得:a≥$\frac{1}{2}$-$\frac{1}{{4e}^{2}}$,不合题意;
③当0<a<$\frac{1}{4}$时,由g′(x)在[e,e2]上为增函数,
故g′(x) 的值域为[g′(e),g′(e2)],即[-a,$\frac{1}{4}$-a].
由g′(x)的单调性和值域知,存在唯一x0∈(e,e2),使g′(x0)=0,且满足:
当x∈(e,x0),时,g′(x)<0,此时g(x)为减函数;
当x∈(x0,e2),时,g′(x)>0,此时g(x)为增函数;
所以,gmax(x)=max{g(e)或g(e2)}与0<a<$\frac{1}{4}$矛盾,不合题意.
综上所述,得a≥$\frac{1}{2}$-$\frac{1}{{4e}^{2}}$.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及分类讨论思想、转化思想,是一道综合题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,AB是圆O的直径,C是圆O上除A、B外的一点,DC⊥平面ABC,四边形CBED为矩形,CD=1,AB=4.
如图,AB是圆O的直径,C是圆O上除A、B外的一点,DC⊥平面ABC,四边形CBED为矩形,CD=1,AB=4.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
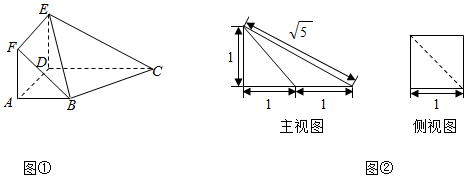 如图,图②为图①空间图形的主视图和侧视图,其中侧视图为正方形.在图①中,设平面BEF与平面ABCD相交于直线l.
如图,图②为图①空间图形的主视图和侧视图,其中侧视图为正方形.在图①中,设平面BEF与平面ABCD相交于直线l.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com