
 如图,AB是圆O的直径,C是圆O上除A、B外的一点,DC⊥平面ABC,四边形CBED为矩形,CD=1,AB=4.
如图,AB是圆O的直径,C是圆O上除A、B外的一点,DC⊥平面ABC,四边形CBED为矩形,CD=1,AB=4.分析 (1)先证明BC⊥平面ACD,再由BC∥ED,得出ED⊥平面ACD;
(2)由V三棱锥C-ADE=V三棱锥E-ACD,利用基本不等式求出三棱锥C-ADE体积的最大值,再利用三棱锥的体积公式计算点C到平面ADE的距离.
解答 解:(1)证明:∵AB是圆O的直径,
∴AC⊥BC,
又DC⊥平面ABC,BC?平面ACD,
∴DC⊥BC,
又AC∩DC=D,
AC?平面ACD,DC?平面ACD,
∴BC⊥平面ACD;
又四边形CBED为矩形,
∴BC∥ED,
∴ED⊥平面ACD;
(2)解:由(1)知,
V三棱锥C-ADE=V三棱锥E-ACD
=$\frac{1}{3}$S△ACD•DE
=$\frac{1}{3}$•$\frac{1}{2}$•AC•CD•DE
=$\frac{1}{6}$•AC•BC≤$\frac{1}{12}$•(AC2+BC2)=$\frac{1}{12}$•AB2=$\frac{1}{12}$×42=$\frac{4}{3}$,
当且仅当AC=BC=2$\sqrt{2}$时等号成立;
∴当AC=BC=2$\sqrt{2}$时,三棱锥C-ADE的体积最大,为$\frac{4}{3}$;
此时,AD=$\sqrt{{1}^{2}{+(2\sqrt{2})}^{2}}$=3,
S△ADE=$\frac{1}{2}$•AD•DE=3$\sqrt{2}$,
设点C到平面ADE的距离为h,则
V三棱锥C-ADE=$\frac{1}{3}•$S△ADE•h=$\frac{4}{3}$;
∴h=$\frac{4}{3}$÷($\frac{1}{3}$×3$\sqrt{2}$)=$\frac{2\sqrt{2}}{3}$.
点评 本题考查了空间中的平行与垂直关系的应用问题,也考查了锥体体积的计算问题,是综合性题目.


 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
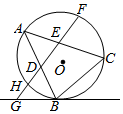 如图,△ABC内接于圆O,分别取AB、AC的中点D、E,连接DE,直线DE交圆O在B点处的切线于G,交圆于H、F两点,若GD=4,DE=2,DF=4.
如图,△ABC内接于圆O,分别取AB、AC的中点D、E,连接DE,直线DE交圆O在B点处的切线于G,交圆于H、F两点,若GD=4,DE=2,DF=4.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | a<b<c | C. | a<c<b | D. | b<c<a |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com