
分析 令a=$\frac{x}{y}$,b=$\frac{y}{z}$,c=$\frac{z}{x}$,x、y、z∈R+,原不等式等价于(x+y-z)(x-y+z)(-x+y+z)≤xyz,再换元,利用基本不等式,即可证明结论.
解答 证明:令a=$\frac{x}{y}$,b=$\frac{y}{z}$,c=$\frac{z}{x}$,x、y、z∈R+,原不等式等价于(x+y-z)(x-y+z)(-x+y+z)≤xyz.
记u=x-y+z,v=x+y-z,ω=-x+y+z,此三数任两个之和都为正数,
∴它们中间最多只有一个不是正数.
如果恰有一个数不是正数,则uvω≤0<xyz,不等式得证.
如果这三个数都大于零,则依均值不等式$\sqrt{uv}$≤$\frac{(x-y+z)+(x+y-z)}{2}$=x.
同理,$\sqrt{vω}$≤y,$\sqrt{ωu}$≤z.于是,uvω≤xyz,不等式成立.
综上所述,原不等式成立.
点评 本题考查不等式的证明,考查基本不等式的运用,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
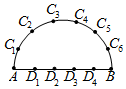 如图,在以AB为直径的半圆周上,有异于A、B的6个点C1、C2、C3、C4、C5、C6,线段AB上有异于A、B的四个点D1、D2、D3、D4.问:
如图,在以AB为直径的半圆周上,有异于A、B的6个点C1、C2、C3、C4、C5、C6,线段AB上有异于A、B的四个点D1、D2、D3、D4.问:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com