Question

3．已知三棱锥A-BCD的所有顶点都在同一个球面上，△BCD是边长为2的正三角形，AC为球O的直径，若该三棱锥的体积为$\frac{{4\sqrt{2}}}{3}$，则该球O的表面积（　　）

• A． 64π
• B． 48π
• C． 32π
• D． 16π

Answer 1

分析 根据题意作出图形，设球心为O，过BCD三点的小圆的圆心为O₁，则OO₁⊥平面BCD，延长CO₁交球于点E，则AE⊥平面BCD，由该三棱锥的体积为$\frac{{4\sqrt{2}}}{3}$，求出AE=$\frac{4\sqrt{6}}{3}$，由AC为球O的直径，求出OO₁=$\frac{1}{2}AE$=$\frac{2\sqrt{6}}{3}$，再求出CO₁=$\frac{2\sqrt{3}}{3}$，从而求出球半径R=OC，进而能求出该球O的表面积．

解答 解：根据题意作出图形：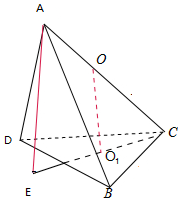
设球心为O，过BCD三点的小圆的圆心为O₁，则OO₁⊥平面BCD，
延长CO₁交球于点E，则AE⊥平面BCD．
∵该三棱锥的体积为$\frac{{4\sqrt{2}}}{3}$，
∴$\frac{1}{3}×AE×{S}_{△BCD}$=$\frac{1}{3}×AE×\frac{1}{2}×2×2×sin60°$=$\frac{4\sqrt{2}}{3}$，
解得AE=$\frac{4\sqrt{6}}{3}$，
∵AC为球O的直径，∴OO₁=$\frac{1}{2}AE$=$\frac{2\sqrt{6}}{3}$，
∵CO₁=$\frac{2}{3}×\sqrt{4-1}$=$\frac{2\sqrt{3}}{3}$，∴球半径R=OC=$\sqrt{（\frac{2\sqrt{6}}{3}）^{2}+（\frac{2\sqrt{3}}{3}）^{2}}$=2．
∴该球O的表面积S=4πR²=16π．
故选：D．

点评 本题考查球的表面积的求法，考查三棱锥的外接球、球的表面积、三棱锥的体积等基础知识，考查推理论证能力、运算求解能力，考查化归与转化思想、函数与方程思想，是中档题．