
已知函数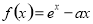 (
(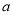 为常数)的图像与
为常数)的图像与 轴交于点
轴交于点 ,曲线
,曲线 在点
在点 处的切线斜率为-1.
处的切线斜率为-1.
(1)求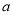 的值及函数
的值及函数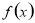 的极值;(2)证明:当
的极值;(2)证明:当 时,
时,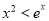 ;
;
(3)证明:对任意给定的正数 ,总存在
,总存在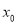 ,使得当
,使得当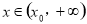 ,恒有
,恒有 .
.
(1) ,极小值为
,极小值为 无极大值;(2)证明见解析;(3)证明见解析.
无极大值;(2)证明见解析;(3)证明见解析.
【解析】
试题分析:
解题思路:(1)利用导数的几何意义求 ,再进一步求极值;(2)构造函数
,再进一步求极值;(2)构造函数 ,即证
,即证 ;
;
(3)结合(2)的结论,对 进行分类讨论.
进行分类讨论.
规律总结:这是一道典型的导函数问题,综合性较强,要求我们要有牢固的基础知识(包括函数的性质、常见解题方法、数形结合等).
试题解析:解法一:(1)由 ,得
,得 .又
.又 ,得
,得 .所以
.所以 .令
.令 ,得
,得 .当
.当 时,
时,  单调递减;当
单调递减;当 时,
时,  单调递增.所以当
单调递增.所以当 时,
时,  取得极小值,且极小值为
取得极小值,且极小值为 无极大值.
无极大值.
(2)令 ,则
,则 .由(1)得
.由(1)得 ,故
,故 在R上单调递增,又
在R上单调递增,又 ,因此,当
,因此,当 时,
时,  ,即
,即 .
.
(3)①若 ,则
,则 .又由(2)知,当
.又由(2)知,当 时,
时,  .所以当
.所以当 时,
时,  .取
.取 ,当
,当 时,恒有
时,恒有 .
.
②若 ,令
,令 ,要使不等式
,要使不等式 成立,只要
成立,只要 成立.而要使
成立.而要使 成立,则只要
成立,则只要 ,只要
,只要 成立.令
成立.令 ,则
,则 .所以当
.所以当 时,
时,  在
在 内单调递增.取
内单调递增.取 ,所以
,所以 在
在 内单调递增.又
内单调递增.又 .易知
.易知 .所以
.所以 .即存在
.即存在 ,当
,当 时,恒有
时,恒有 .
.
综上,对任意给定的正数c,总存在 ,当
,当 时,恒有
时,恒有 .
.
解法二:(1)同解法一
(2)同解法一
(3)对任意给定的正数c,取
由(2)知,当x>0时, ,所以
,所以
当 时,
时, 
因此,对任意给定的正数c,总存在 ,当
,当 时,恒有
时,恒有 .
.
考点:1.导数的几何意义;2.导数在研究函数中的应用.


科目:高中数学 来源:2015数学一轮复习迎战高考:2-11导数的应用(解析版) 题型:选择题
函数f(x)=ex-x(e为自然对数的底数)在区间[-1,1]上的最大值是( )
A.1+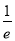 B.1 C.e+1 D.e-1
B.1 C.e+1 D.e-1
查看答案和解析>>
科目:高中数学 来源:2015数学一轮复习迎战高考:10-2排列与组合(解析版) 题型:选择题
[2014·衡阳质检]4位同学每人从甲、乙、丙3门课程中选修1门,则恰有2人选修课程甲的不同选法共有( )
A.12种 B.24种 C.30种 D.36种
查看答案和解析>>
科目:高中数学 来源:2015数学一轮复习迎战高考10-1分类加法计数原理与分步乘法计数原理(解析版) 题型:选择题
[2014·济南调研]用0,1,2,3,4,5六个数字组成无重复数字的四位数,若把每位数字比其左邻的数字小的数叫做“渐降数”,则上述四位数中“渐降数”的个数为( )
A.14 B.15 C.16 D.17
查看答案和解析>>
科目:高中数学 来源:2015数学一轮复习迎战高考1-3简单逻辑联结词、全称量词与存在量词(解析版) 题型:选择题
[2014·河南洛阳模拟]下列命题中的假命题是( )
A.?x∈R,2x-1>0 B.?x∈N*,(x-1)2>0
C.?x∈R,lgx<1 D.?x∈R,tanx=2
查看答案和解析>>
科目:高中数学 来源:2015届黑龙江省高二下学期期末考试理科数学试卷(解析版) 题型:填空题
已知函数f(x)= , (a是常数且a>0).对于下列命题:
, (a是常数且a>0).对于下列命题:
①函数f(x)的最小值是-1;
②函数f (x)在R上是单调函数;
③若f(x)>0在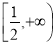 上恒成立,则a的取值范围是a>1;
上恒成立,则a的取值范围是a>1;
④对任意的x1<0,x2<0且x1≠x2,恒有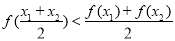
其中正确命题的序号是__________(写出所有正确命题的序号).
查看答案和解析>>
科目:高中数学 来源:2015届黑龙江省高二下学期期末考试理科数学试卷(解析版) 题型:选择题
在同一坐标系中画出函数y=logax,y=ax,y=x+a的图象,可能正确的是( ).
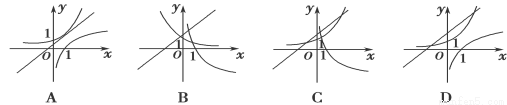
查看答案和解析>>
科目:高中数学 来源:2015届黑龙江省高二下学期期末考试文科数学试卷(解析版) 题型:填空题
若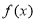 是定义在R上的奇函数,且满足
是定义在R上的奇函数,且满足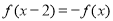 ,给出下列4个结论:
,给出下列4个结论:
(1)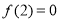 ; (2)
; (2)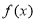 是以4为周期的函数;
是以4为周期的函数;
(3)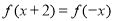 ; (4)
; (4)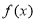 的图像关于直线
的图像关于直线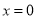 对称;
对称;
其中所有正确结论的序号是 .
查看答案和解析>>
科目:高中数学 来源:2015届黑龙江省高二下学期期末考试文科数学试卷(解析版) 题型:解答题
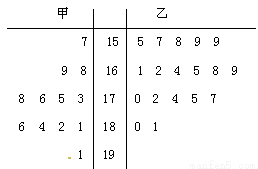
某学校准备参加市运动会,对本校甲、乙两个田径队中30名跳高运动员进行了测试,并用茎叶图表示出本次测试30人的跳高成绩(单位cm),跳高成绩在175cm以上(包括175cm)定义为“合格”,成绩在175以下(不包括175cm)定义为“不合格”
(1)求甲队队员跳高成绩的中位数
(2)如果用分层抽样的方法从甲、乙两队所有的运动员中共抽取5人,则5人中“合格”与“不合格”的人数各为多少?
(3)从甲队178cm以上(包括178cm)选取2人,至少有一人在186cm以上(包括186cm)的概率为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com