Question

14．把平面直角坐标系xOy中，点A（2，0），点B在单位圆上，∠AOB=θ（0＜θ＜π）．
（1）若点B（-$\frac{3}{5}$，$\frac{4}{5}$），求tan（$\frac{π}{4}$-θ）的值；
（2）若$\overrightarrow{OA}$+$\overrightarrow{OB}$=$\overrightarrow{OC}$，$\overrightarrow{OB}$•$\overrightarrow{OC}$=$\frac{33}{17}$，求cos（$\frac{π}{3}$+θ）的值．

Answer 1

分析 （1）由已知可得tanθ，然后展开两角差的正确求解；
（2）利用向量的数量积运算求得cosθ，进一步展开两角和的余弦求解．

解答 解：（1）点B（-$\frac{3}{5}$，$\frac{4}{5}$），如图：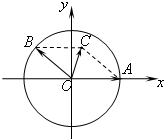
则tanθ=-$\frac{4}{3}$，
∴tan（$\frac{π}{4}-θ$）=$\frac{tan\frac{π}{4}-tanθ}{1+tan\frac{π}{4}tanθ}$=$\frac{1-tanθ}{1+tanθ}$=$\frac{1-（-\frac{4}{3}）}{1-\frac{4}{3}}=-7$；
（2）$\overrightarrow{OA}=（2，0）$，$\overrightarrow{OB}$=（cosθ，sinθ）．
∴$\overrightarrow{OC}=\overrightarrow{OA}+\overrightarrow{OB}$=（2+cosθ，sinθ）．
∴$\overrightarrow{OB}•\overrightarrow{OC}$=cosθ（2+cosθ）+sin2θ=2cosθ+1=$\frac{33}{17}$．
∴cosθ=$\frac{8}{17}$；
又θ∈（0，π），
∴sinθ=$\sqrt{1-co{s}^{2}θ}$=$\frac{15}{17}$．
∴cos（$\frac{π}{3}+θ$）=cos$\frac{π}{3}$cosθ-sin$\frac{π}{3}$sinθ
=$\frac{1}{2}×\frac{8}{17}-\frac{\sqrt{3}}{2}×\frac{15}{17}$=$\frac{8-15\sqrt{3}}{34}$．

点评 考查平面向量的数量积运算，考查三角函数的定义，两角差的正切公式，两角和的余弦公式，是中档题．