
【题目】(2015·新课标I卷)函数f(x)=cos(![]() x+
x+![]() )的部分图像如图所示,则f(x)的单调递减区间为( )
)的部分图像如图所示,则f(x)的单调递减区间为( )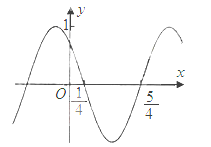
A.(k![]() -
-![]() ,k
,k![]() +
+![]() ), k
), k![]() Z
Z
B.(2k![]() -
-![]() ,2k
,2k![]() +
+![]() ),k
),k![]() Z
Z
C.(k-![]() ,k+
,k+![]() ), k
), k![]() Z
Z
D.(2k-![]() ,2k+
,2k+![]() ),k
),k![]() Z
Z
【答案】D
【解析】由五点作图知, 1 4 ω + φ = π 2 5 4 ω + φ = 3 π 2 ,解得 ω = π , φ = π 4 ,所以f(x)=cos( π x+ π 4 ),令2k π < π x+ π 4 ,k ∈ Z, 解得2k- 1 4 <x<2k+ 3 4 ,k ∈ Z ,故单调递减区间为(2k- 1 4 ,2k+ 3 4 ),k ∈ Z ,故选D。
本题考查函数y=Acos(ωx+φ)的图像与性质,先利用五点作图法列出关于 ω , φ 方程,求出 ω , φ 或利用利用图像先求出周期,用周期公式求出 ω ,利用特殊点求出 φ ,再利用复合函数单调性求其单调递减区间,是中档题,正确求 ω , φ 使解题的关键.


科目:高中数学 来源: 题型:
【题目】![]() 如图,长方体ABCD-A1B1C1D1中,AB=16,BC=10,AA1=8,点E,F分别在A1B1,D1C1上,A1E=D1F=4.过点E,F的平面
如图,长方体ABCD-A1B1C1D1中,AB=16,BC=10,AA1=8,点E,F分别在A1B1,D1C1上,A1E=D1F=4.过点E,F的平面![]() 与此长方体的面相交,交线围成一个正方形。
与此长方体的面相交,交线围成一个正方形。
(1)(I)在图中画出这个正方形(不必说明画法与理由);
(2)(II)求平面 把该长方体分成的两部分体积的比值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 如图,长方形ABCD的边AB=2,BC=1,O是AB的中点,点P沿着边BC,CD与DA运动,记
如图,长方形ABCD的边AB=2,BC=1,O是AB的中点,点P沿着边BC,CD与DA运动,记![]() BOP=x,将动P到A、B两点距离之和表示为x的函数f(x),则y=f(x)的图像大致为()
BOP=x,将动P到A、B两点距离之和表示为x的函数f(x),则y=f(x)的图像大致为()
A.
B.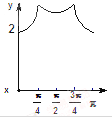
C.
D.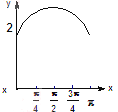
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 设函数f(x)=emx+x2-mx
设函数f(x)=emx+x2-mx
(1)(I)证明:f(x)在(-![]() ,0)单调递减,在(0,+
,0)单调递减,在(0,+![]() )单调递增;
)单调递增;
(2)(II)若对于任意x1 , x2![]() [-1,1],都有|f(x1)-f(x2)|
[-1,1],都有|f(x1)-f(x2)|![]() e-1,求m的取值范围。
e-1,求m的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·新课标I卷)在直角坐标系xoy中,曲线C:y=![]() 与直线y=kx+a(a>0)交与M,N两点,
与直线y=kx+a(a>0)交与M,N两点,
(1)当k=0时,分别求C在点M和N处的切线方程;
(2)y轴上是否存在点P , 使得当k变动时,总有∠OPM=∠OPN?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 的对边分别为
的对边分别为![]() 且
且![]() 为锐角,问:(1)证明: B - A =
为锐角,问:(1)证明: B - A = ![]() ,(2)求 sin A + sin C 的取值范围
,(2)求 sin A + sin C 的取值范围
(1)(1)证明:![]()
(2)(2)求![]() 的取值范围
的取值范围
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·四川)如图,四边形ABCD和ADPQ均为正方形,它们所在的平面互相垂直,动点M在线段PQ上,E、F分别为AB、BC的中点。设异面直线EM与AF所成的角为![]() ,则cos
,则cos![]() 的最大值为 .
的最大值为 .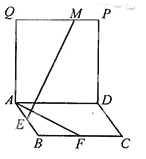
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在几何体ABCDE中,四边形ABCD是矩形,AB⊥平面BEC,BE⊥EC,AB=BE=EC=2,G,F分别是线段BE,DC的中点.
(Ⅰ)求证:BE//平面ADE ;
(Ⅱ)求平面AEF与平面BEC所成锐二面角的余弦值.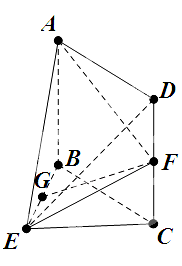
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com