
分析 (1)由奇函数的定义,可得f(-x)+f(x)=0,化简整理,解方程可得m的值(也可通过f(0)=0);
(2)运用单调性的定义证明,分取值、作差、变形和定符号、下结论等;
(3)由于f(x)为奇函数且在R上为增函数,由题意可得k•3x<-3x+9x+2即k<-1+3x+$\frac{2}{{3}^{x}}$,运用基本不等式求得右边函数的最小值,即可得到所求k的范围.
解答 解:(1)函数f(x)=m-$\frac{2}{{2}^{x}+1}$为奇函数,
可得f(-x)=m-$\frac{2}{{2}^{-x}+1}$=m-$\frac{2•{2}^{x}}{1+{2}^{x}}$,且f(-x)+f(x)=0,
∴2m-$\frac{2(1+{2}^{x})}{1+{2}^{x}}$=2m-2=0(注:通过f(0)=0求可以,但要验证)
∴m=1;
(2)证明:设x1,x2∈R,x1<x2,
则f(x1)-f(x2)=(m-$\frac{2}{1+{2}^{{x}_{1}}}$)-(m-$\frac{2}{1+{2}^{{x}_{2}}}$)=$\frac{2}{1+{2}^{{x}_{2}}}$-$\frac{2}{1+{2}^{{x}_{1}}}$=$\frac{2({2}^{{x}_{1}}-{2}^{{x}_{2}})}{(1+{2}^{{x}_{1}})(1+{2}^{{x}_{2}})}$
∵x1,x2∈R,x1<x2,
∴0<2${\;}^{{x}_{1}}$<2${\;}^{{x}_{2}}$,即2${\;}^{{x}_{1}}$-2${\;}^{{x}_{2}}$<0,
∴f(x1)-f(x2)<0即f(x1)<f(x2).
则f(x)在R上为增函数.
(3)由于f(x)为奇函数且在R上为增函数,
由f(k•3x)+f(3x-9x-2)<0得:f(k•3x)<-f(3x-9x-2)=f(-3x+9x+2),
∴k•3x<-3x+9x+2即k<-1+3x+$\frac{2}{{3}^{x}}$,
由3x>0,可得y=-1+3x+$\frac{2}{{3}^{x}}$≥-1+2$\sqrt{{3}^{x}•\frac{2}{{3}^{x}}}$=2$\sqrt{2}$-1,
当且仅当3x=$\frac{2}{{3}^{x}}$,即x=log3$\sqrt{2}$时,取得最小值2$\sqrt{2}$-1,
则k<2$\sqrt{2}$-1.
故实数k的取值范围是(-∞,2$\sqrt{2}$-1).
点评 本题考查函数的奇偶性和单调性的判断和应用,注意运用定义法,考查不等式恒成立问题的解法,注意运用参数分离和基本不等式求最值,考查化简整理的运算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 抛物线 | B. | 双曲线 | C. | 椭圆 | D. | 圆 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
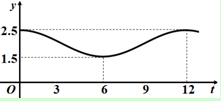 某企业一天中不同时刻的用电量y(万千瓦时)关于时间t(小时,0≤t≤24)的函数y=f(t)近似满足f(t)=Asin(ωt+φ)+B,(A>0,ω>0,0<φ<π).如图是函数y=f(t)的部分图象(t=0对应凌晨0点).
某企业一天中不同时刻的用电量y(万千瓦时)关于时间t(小时,0≤t≤24)的函数y=f(t)近似满足f(t)=Asin(ωt+φ)+B,(A>0,ω>0,0<φ<π).如图是函数y=f(t)的部分图象(t=0对应凌晨0点).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 简单随机抽样 | B. | 按性别分层抽样 | C. | 按年级分层抽样 | D. | 系统抽样 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{8}{25}$ | B. | $\frac{9}{25}$ | C. | $\frac{18}{25}$ | D. | $\frac{17}{25}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com