
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 利用y=Asin(ωx+φ)的周期等于 T=$\frac{2π}{ω}$,y=|Asin(ωx+φ)|的周期为$\frac{π}{ω}$,y=Atan(ωx+φ)的周期为$\frac{π}{ω}$,得出结论.
解答 解:∵函数y=sin|x|不是周期函数,y=|sinx|是周期等于π的函数,
y=sin(2x+$\frac{2π}{3}$)的周期等于$\frac{2π}{2}$=π,y=tan(2x+$\frac{2π}{3}$)的周期为$\frac{π}{2}$,
故这些函数中,最小正周期为π的函数的个数为2,
故选:B.
点评 本题主要考查三角函数的周期性及其求法,利用了y=Asin(ωx+φ)的周期等于 T=$\frac{2π}{ω}$,y=|Asin(ωx+φ)|的周期为$\frac{π}{ω}$,y=Atan(ωx+φ)的周期为$\frac{π}{ω}$,属于基础题.


 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,2] | B. | $({0,\frac{1}{2}}]$ | C. | $[{\frac{1}{2},2}]$ | D. | (0,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 存在满足x<y的x,y∈[a,b]使得f(x)>f(y) | |
| B. | 不存在x,y∈[a,b]满足x<y且f(x)≤f(y) | |
| C. | 对任意满足x<y的x,y∈[a,b]都有f(x)>f(y) | |
| D. | 存在满足x<y的x,y∈[a,b]都有f(x)≤f(y) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
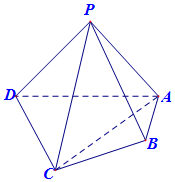 如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,PA⊥PD,PA=PD,AB⊥AD,AB=1,AD=2,AC=CD=$\sqrt{5}$.
如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,PA⊥PD,PA=PD,AB⊥AD,AB=1,AD=2,AC=CD=$\sqrt{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({\frac{{\sqrt{3}}}{2}})$ | B. | $-\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | $-\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,0)∪(4,+∞) | B. | (0,2)∪(4,+∞) | C. | (-∞,0)∪(0,4) | D. | (0,2)∪(2,4) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com