
| A. | 83 | B. | 93 | C. | 103 | D. | 113 |
分析 利用二项式定理可得:a=C${\;}_{100}^{0}$+C${\;}_{100}^{1}$•8+…+C${\;}_{100}^{99}$•899+C${\;}_{100}^{100}$•8100=(1+8)100=(10-1)100,展开可得:a-1=103×$(1{0}^{97}-{∁}_{100}^{1}•1{0}^{96}+$…-${∁}_{100}^{97}$+494),即可得出结论.
解答 解:∵a=C${\;}_{100}^{0}$+C${\;}_{100}^{1}$•8+…+C${\;}_{100}^{99}$•899+C${\;}_{100}^{100}$•8100=(1+8)100=(10-1)100
=$1{0}^{100}+{∁}_{100}^{1}$1099×(-1)+…+${∁}_{100}^{98}×1{0}^{2}$-${∁}_{100}^{99}$×10+1,
∴a-1=103×$(1{0}^{97}-{∁}_{100}^{1}•1{0}^{96}+$…-${∁}_{100}^{97}$+494),
∴103|(a-1),
则b=103.
故选:C.
点评 本题考查了二项式定理的应用、整除的方法,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源:2017届宁夏高三上月考一数学(文)试卷(解析版) 题型:解答题
已知函数 .
.
(1)当 时,求函数
时,求函数 在
在 上的最小值和最大值;
上的最小值和最大值;
(2)当 时,讨论函数
时,讨论函数 的单调性;
的单调性;
(3)是否存在实数 ,对任意的
,对任意的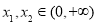 ,且
,且 ,都有
,都有 恒成立,若存在,求出
恒成立,若存在,求出 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x | 3 | 6 | 9 | 8 | 9 |
| y | 12 | 10 | 8 | 8 | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com