
分析 ?x1,x2∈R,使得f(x2)≤g(x1)成立,等价于f(x)min≤g(x)max,利用导数可求得f(x)的最小值,根据二次函数的性质可求得g(x)的最大值,代入上述不等式即可求得答案.
解答 解:?x1,x2∈R,使得f(x2)≤g(x1)成立,等价于f(x)min≤g(x)max,
f′(x)=ex+xex=(1+x)ex,
当x<-1时,f′(x)<0,f(x)递减,当x>-1时,f′(x)>0,f(x)递增,
所以当x=-1时,f(x)取得最小值f(x)min=f(-1)=-$\frac{1}{e}$;
当x=-1时g(x)取得最大值为g(x)max=g(-1)=a,
所以-$\frac{1}{e}$≤a,即实数a的取值范围是a≥-$\frac{1}{e}$,
故答案为:[-$\frac{1}{e}$,+∞).
点评 本题考查二次函数的性质及利用导数求函数的最值,考查“能成立”问题的处理方法,解决该题的关键是把问题转化为求函数的最值问题解决.


科目:高中数学 来源: 题型:解答题
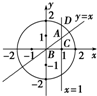 直线x=1,y=x,将圆x2+y2=4分成A,B,C,D四个区域,如图用五种不同的颜色给他们涂色,要求共边的两区域颜色互异,每个区域只涂一种颜色,共有多少种不同的涂色方法?
直线x=1,y=x,将圆x2+y2=4分成A,B,C,D四个区域,如图用五种不同的颜色给他们涂色,要求共边的两区域颜色互异,每个区域只涂一种颜色,共有多少种不同的涂色方法?查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2012 | B. | 2012 | C. | 4024 | D. | 4022 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com