
| A. | 4条 | B. | 3条 | C. | 2条 | D. | 1条 |
分析 求出双曲线x2-$\frac{{y}^{2}}{4}$=1的渐近线方程y=±2x,结合双曲线的性质讨论,直线l与双曲线相切,有两条,一条为斜率不存在的和另一条斜率存在,由判别式为0,解得斜率;直线l与渐近线平行的有两条,共有4条.
解答 解:双曲线x2-$\frac{{y}^{2}}{4}$=1的渐近线方程为y=±2x,
①直线l:x=1与双曲线只有一个公共点;
②过点P (1,1)平行于渐近线y=±2x时,直线l与双曲线只有一个公共点;
③设过P的切线方程为y-1=k(x-1)与双曲线x2-$\frac{{y}^{2}}{4}$=1联立,
可得(4-k2)x2-2k(1-k)x-(1-k)2-4=0,
由△=0,即4k2(1-k)2+4(4-k2)[(1-k)2-4]=0,解得k=$\frac{5}{2}$,直线l的条数为1.
综上可得,直线l的条数为4.
故选:A.
点评 本题以双曲线为载体,主要考查了直线与双曲线的位置关系,突出考查了双曲线的几何性质,属于中档题和易错题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
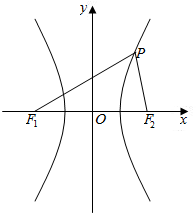 已知双曲线的中心在坐标原点,焦点在x轴上,F1,F2分别为左、右焦点,双曲线的右支上有一点P,∠F1PF2=$\frac{π}{3}$,且△PF1F2的面积为2$\sqrt{3}$,又双曲线的离心率为2,求该双曲线的方程.
已知双曲线的中心在坐标原点,焦点在x轴上,F1,F2分别为左、右焦点,双曲线的右支上有一点P,∠F1PF2=$\frac{π}{3}$,且△PF1F2的面积为2$\sqrt{3}$,又双曲线的离心率为2,求该双曲线的方程.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 收缩压范围 | 89.5~104.4 | 104.5~119.4 | 119.5~134.4 | 134.5~149.4 | 149.5~164.4 | 164.5~179.4 |
| 人数 | 24 | 62 | 72 | 26 | 12 | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com