
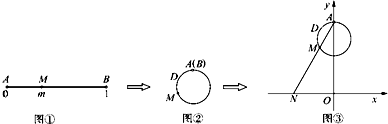
 ��ͼչʾ��һ�������䣨0��1����ʵ����R��ӳ����̣����䣨0��1���е�ʵ��m��Ӧ�����ϵĵ�M����ͼ�٣����߶�ABΧ��һ��Բ��ʹ���˵�A��Bǡ���غϣ���ͼ�ڣ��ٽ����Բ����ƽ��ֱ������ϵ�У�ʹ��Բ����y���ϣ���A������Ϊ��0��1������ͼ�α仯�����У�ͼ�����߶�AM�ij��ȶ�Ӧ��ͼ���еĻ�ADM�ij��ȣ���ͼ�ۣ�ͼ����ֱ��AM��x�ύ�ڵ�N��n��0������m�������n������f��m��=n��
��ͼչʾ��һ�������䣨0��1����ʵ����R��ӳ����̣����䣨0��1���е�ʵ��m��Ӧ�����ϵĵ�M����ͼ�٣����߶�ABΧ��һ��Բ��ʹ���˵�A��Bǡ���غϣ���ͼ�ڣ��ٽ����Բ����ƽ��ֱ������ϵ�У�ʹ��Բ����y���ϣ���A������Ϊ��0��1������ͼ�α仯�����У�ͼ�����߶�AM�ij��ȶ�Ӧ��ͼ���еĻ�ADM�ij��ȣ���ͼ�ۣ�ͼ����ֱ��AM��x�ύ�ڵ�N��n��0������m�������n������f��m��=n��| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2�� |
| 1 |
| 2�� |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 3 |
| 4 |
| 1 |
| 4 |
| 3 |
| 4 |


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
| 1 |
| 2 |
| �� |
| 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| a+m |
| b+m |
| a |
| b |
| 2 |
| sinx |
| 2 |
| a |
| x |
| c |
| y |
| 2 |
| 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
|
| a+b+c |
| a |
| A��1 | B��2 | C��-1 | D��-2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| A������a��b����2a��2b-1���ķ����� |
| B����?a�ʣ�0��+�ޣ�������y=ax�ڶ������ڵ����������ķ� |
| C�������Ǻ���y=sinx��һ�����ڡ���2���Ǻ���y=sin2x��һ�����ڡ� |
| D����x2+y2=0���ǡ�xy=0���ı�Ҫ������ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com