
| A. | f(x)=|sinx| | B. | f(x)=ln$\frac{2-x}{2+x}$ | C. | f(x)=$\frac{1}{2}$(ex-e-x) | D. | f(x)=ln($\sqrt{{x}^{2}+1}$-x) |
分析 根据题意,依次分析4个选项所给函数的奇偶性与单调性,是否满足题意,即可得答案.
解答 解:根据题意,依次分析选项:
对于A、f(x)=|sinx|,有f(-x)=|sin(-x)|=|sinx|=f(x),为偶函数,不符合题意,
对于B、f(x)=ln$\frac{2-x}{2+x}$,有$\frac{2-x}{2+x}$>0,解可得-2<x<2,即其定义域为(-2,2),关于原点对称,又由f(-x)=ln$\frac{2+x}{2-x}$=-f(x),为奇函数,
令t=$\frac{2-x}{2+x}$=-1+$\frac{4}{x+2}$,在区间(-1,1)上为减函数,而y=lnt为增函数,
而f(x)=ln$\frac{2-x}{2+x}$在区间(-1,1)上为减函数,不符合题意,
对于C、f(x)=$\frac{1}{2}$(ex-e-x),其定义域为R,关于原点对称,又由f(-x)=$\frac{1}{2}$(e-x-ex)=-f(x),为奇函数,
函数y=ex为增函数,而函数y=e-x为减函数,
故函数f(x)=$\frac{1}{2}$(ex-e-x)在区间(-1,1)上为增函数,符合题意,
对于D、f(x)=ln($\sqrt{{x}^{2}+1}$-x),有$\sqrt{{x}^{2}+1}$-x>0,解可得x∈R,其定义域为R,关于原点对称,又由f(-x)=-f(x),为奇函数;
令t=$\sqrt{{x}^{2}+1}$-x=$\frac{1}{\sqrt{{x}^{2}+1}+x}$,在区间(-1,1)为减函数,而y=lnt为增函数,
故f(x)=ln($\sqrt{{x}^{2}+1}$-x)在区间(-1,1)上为减函数,不符合题意,
故选:C.
点评 本题考查函数奇偶性与单调性的判断,关键是掌握函数奇偶性与单调性的判定方法,尤其复合函数单调性的判断方法.


科目:高中数学 来源: 题型:选择题
| A. | [-1,1] | B. | [-$\frac{2\sqrt{3}}{3}$,$\frac{2\sqrt{3}}{3}$] | C. | [1,$\sqrt{2}$] | D. | [$\frac{2\sqrt{3}}{3}$,$\sqrt{2}$] |
查看答案和解析>>
科目:高中数学 来源:2017届湖南长沙长郡中学高三上周测十二数学(理)试卷(解析版) 题型:解答题
在一个盒子里装有6张卡片,上面分别写着如下定义域为 的函数:
的函数:
 ,
,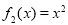 ,
,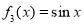 ,
,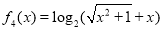 ,
, ,
,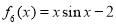 .
.
(1)现在从盒子中任意取两张卡片,记事件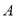 为“这两张卡片上函数相加,所得新函数是奇函数”,求事件
为“这两张卡片上函数相加,所得新函数是奇函数”,求事件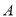 的概率;
的概率;
(2)从盒中不放回逐一抽取卡片,若取到一张卡片上的函数是偶函数则停止抽取,否则继续进行,记停止时抽取次数为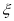 ,写出
,写出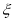 的分布列,并求其数学期望
的分布列,并求其数学期望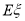 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | l | C. | -l | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | l | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图给出的是计算1+$\frac{1}{3}$+$\frac{1}{5}$+…+$\frac{1}{2017}$的值的一个程序框图,则判断框内应填入的条件是( )
如图给出的是计算1+$\frac{1}{3}$+$\frac{1}{5}$+…+$\frac{1}{2017}$的值的一个程序框图,则判断框内应填入的条件是( )| A. | i≤1009 | B. | i>1009 | C. | i≤1010 | D. | i>1010 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com