Question

16．随着移动互联网的快速发展，基于互联网的共享单车应用而生，某市场研究人员为了了解共享单车运营公司M的经营状况，对该公司最近六个月内的市场占有率进行了统计，并绘制了相应的折线图．
（Ⅰ）由折线图可以看出，可用线性回归模型拟合月度市场占有率y与月份代码x之间的关系，求y关于x的线性回归方程，并预测M公司2017年4月份（即x=7时）的市场占有率；
（Ⅱ）为进一步扩大市场，公司拟再采购一批单车．现有采购成本分别为1000元/辆和1200元/辆的A、B两款车型可供选择，按规定每辆单车最多使用4年，但由于多种原因（如骑行频率等）会导致车辆报废年限不相同．考虑到公司运营的经济效益，该公司决定先对两款车型的单车各100辆进行科学模拟测试，得到两款单车使用寿命频数表如下：

报废年限 车型	1年	2年	3年	4年	总计
A	20	35	35	10	100
B	10	30	40	20	100

经测算，平均每辆单车每年可以带来收入500元，不考虑除采购成本之外的其他成本，假设每辆单车的使用寿命都是整数年，且以频率作为每辆单车使用寿命的概率．如果你是M公司的负责人，以每辆单车产生利润的期望值为决策依据，你会选择采购哪款车型？
（参考公式：回归直线方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$，其中$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overrightarrow{x}）^{2}}$，$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$）

Answer 1

分析 （Ⅰ）求出回归系数，可得回归方程，即可得出结论；
（Ⅱ）分别计算相应的数学期望，即可得出结论．

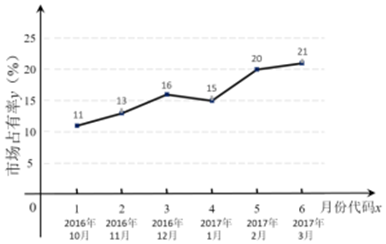
解答 解：（Ⅰ）由题意，$\overline{x}$=3.5，$\overline{y}$=16，$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overrightarrow{x}）^{2}}$=$\frac{35}{17.5}$=2，$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$=16-2×3.5=9，
∴$\stackrel{∧}{y}$=2x+9，
x=7时，$\stackrel{∧}{y}$=2×7+9=23，即预测M公司2017年4月份（即x=7时）的市场占有率为23%；
（Ⅱ）由频率估计概率，每辆A款车可使用1年，2年，3年、4年的概率分别为0.2，0.35，0.35，0.1，
∴每辆A款车的利润数学期望为（500-1000）×0.2+（1000-1000）×0.35+（1500-1000）×0.35+（2000-1000）×0.1=175元；
每辆B款车可使用1年，2年，3年、4年的概率分别为0.1，0.3，0.4，0.2，
∴每辆B款车的利润数学期望为（500-1200）×0.1+（1000-1200）×0.3+（1500-1200）×0.4+（2000-1200）×0.2=150元；
∵175＞150，
∴应该采购A款车．

点评 本题考查数学知识在实际生活中的应用，考查学生的阅读能力，对数据的处理能力，属于中档题．