
分析 利用函数y=sin2x与y=cosx,建立方程,求出三角方程的解即可得到答案.
解答 解:由函数y=sin2x与y=cosx,可得:sin2x=cosx,
即2sinxcosx=cosx,当cosx=0时,x=-$\frac{π}{2}$,$\frac{π}{2}$,$\frac{3π}{2}$,
当cosx≠0时,sinx=$\frac{1}{2}$,解得x=$\frac{π}{6}$,$\frac{5π}{6}$,
在区间[-π,2π]上的函数y=sin2x的图象与y=cosx的图象交点的横坐标之和等于:
-$\frac{π}{2}$+$\frac{π}{2}$+$\frac{3π}{2}$+$\frac{π}{6}$+$\frac{5π}{6}$=$\frac{5π}{2}$π.
给答案为:$\frac{5π}{2}$.
点评 本题考查正弦函数与余弦函数的图象,作出函数y=sin2x与y=cosx在区间[-π,2π]上的图象是关键,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
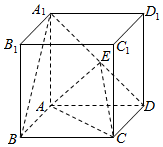 如图,在底面是菱形的四棱柱ABCD-A1B1C1D1中,∠ABC=60°,AA1=AC=2,A1B=A1D=2$\sqrt{2}$,点E在A1D上.
如图,在底面是菱形的四棱柱ABCD-A1B1C1D1中,∠ABC=60°,AA1=AC=2,A1B=A1D=2$\sqrt{2}$,点E在A1D上.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,将平面直角坐标系中的格点(横、纵坐标均为整点的点)按如下规则标上数字标签:点(0,0)处标0,点(1,0)处标1,点(1,-1)处标2,点(0,-1)处标3,点(-1,-1)处标4,点(-1,0)处标5,点(-1,1)处标6,点(0,1)处标7,依此类推,则标签20172的格点坐标 为(1009,1008).
如图,将平面直角坐标系中的格点(横、纵坐标均为整点的点)按如下规则标上数字标签:点(0,0)处标0,点(1,0)处标1,点(1,-1)处标2,点(0,-1)处标3,点(-1,-1)处标4,点(-1,0)处标5,点(-1,1)处标6,点(0,1)处标7,依此类推,则标签20172的格点坐标 为(1009,1008).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
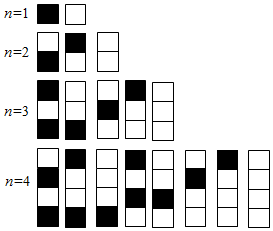 给n个自上而下相连的正方形着黑色或白色.当n≤4时,在所有不同的着色方案中,黑色正方形互不相邻的着色方案如图所示,由此推断,当n=6时,至少有两个黑色正方形相邻的着色方案共有( )种.
给n个自上而下相连的正方形着黑色或白色.当n≤4时,在所有不同的着色方案中,黑色正方形互不相邻的着色方案如图所示,由此推断,当n=6时,至少有两个黑色正方形相邻的着色方案共有( )种.| A. | 21 | B. | 32 | C. | 43 | D. | 54 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
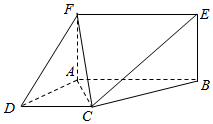 如图,已知四边形ABEF为矩形,四边形ABCD为直角梯形,平面ABEF⊥平面ABCD,∠BAD=90°,AB∥CD,AF=BC=2,CD=3,AB=4.
如图,已知四边形ABEF为矩形,四边形ABCD为直角梯形,平面ABEF⊥平面ABCD,∠BAD=90°,AB∥CD,AF=BC=2,CD=3,AB=4.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com