练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    19．已知如下等式：
    2+4=6；
    8+10+12=14+16；
    18=20+22+24=26+28+30；
    …
    以此类推，则2018出现在第31个等式中．

    分析 从已知等式分析，发现规律为：各等式首项分别为2×1，2（1+3），2（1+3+5），…，即可得出结论．

    解答 解：①2+4=6；  
    ②8+10+12=14+16；
    ③18+20+22+24=26+28+30，…
    其规律为：各等式首项分别为2×1，2（1+3），2（1+3+5），…，
    所以第n个等式的首项为2[1+3+…+（2n-1）]=2×$\frac{n（1+2n-1）}{2}$=2n2，
    当n=31时，等式的首项为2×312=1932，
    当n=32时，等式的首项为2×322=2048，
    所以2018在第31个等式中，
    故答案为：31

    点评 本题考查归纳推理，难点是根据能够找出数之间的内在规律，考查观察、分析、归纳的能力，是基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    9．函数y=sin（ωx+θ-$\frac{π}{6}$）的最小正周期为π，且其图象向左平移$\frac{π}{6}$单位得到的函数为奇函数，则θ的一个可能值是（　　）
    A．$\frac{π}{3}$B．-$\frac{π}{3}$C．$\frac{π}{6}$D．-$\frac{π}{6}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．二项式${（{\sqrt{x}-\frac{1}{{\sqrt{x}}}}）^{12}}$展开式中，x3的系数是（　　）
    A．-495B．-220C．495D．220

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    7．设向量$\overrightarrow a，\vec b$满足$|\overrightarrow a|=|\vec b|=1，|2\overrightarrow a-\vec b|=2$，则$|\overrightarrow a+\vec b|$=$\frac{\sqrt{10}}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．已知函数f（x）=（2x-x2）ex，给以下四个结论：①f（x）＞0的解集为{x|0＜x＜2}；②$f（{-\sqrt{2}}）$是极小值，$f（{\sqrt{2}}）$是极大值；③f（x）有极小值，但无最小值；④f（x）有极小值，也有最小值．其中正确的是（　　）
    A．①②B．①②③C．①②④D．②④

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    4．若复数z=log2（x2-3x-2）+ilog2（x-3）为实数，则实数x的值为4．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．若数列{an}满足a1=1，an+1=nan+1，则第5项a5=（　　）
    A．5B．65C．89D．206

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．在△ABC中，角A，B，C的对边分别为a，b，c，且atanC=2csinA．
    （I） 求角C的大小；
    （II） 求sinA+sinB的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

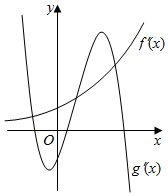    9．定义在R上的函数f（x）和g（x），其各自导函数f′（x）f和g′（x）的图象如图所示，则函数F（x）=f（x）-g（x）极值点的情况是（　　）
    A．只有三个极大值点，无极小值点B．有两个极大值点，一个极小值点
    C．有一个极大值点，两个极小值点D．无极大值点，只有三个极小值点

    查看答案和解析>>

    同步练习册答案