
分析 (1)直接根据$\frac{1-x}{1+x}$>0求得函数的定义域;
(2)先确定函数的单调性,再根据单调性得出k的取值范围;
(3)运用二分法确定函数零点的区间;
解答 解:(1)∵f(x)=2+log2$\frac{1-x}{1+x}$,
∴$\frac{1-x}{1+x}$>0,解得x∈(-1,1),
所以,f(x)的定义域为(-1,1);
(2)根据方程f(x)=2+log2$\frac{1-x}{1+x}$=log2k,
所以,$\frac{k}{4}$=$\frac{1-x}{1+x}$,x∈(-1,-$\frac{1}{2}$),
记g(x)=$\frac{1-x}{1+x}$=-1+$\frac{2}{x+1}$,在x∈(-1,-$\frac{1}{2}$)上单调递减,
因此,g(x)的值域为(3,+∞),
所以,$\frac{k}{4}$∈(3,+∞),解得k∈(12,+∞),
即实数k的取值范围为:(12,+∞);
(3)g(x)=f(x)-(x+1)=log2$\frac{1-x}{1+x}$-x+1,
由(2)可知f(x)单调递减,所以g(x)也单调递减,
且g(0)=1>0,g($\frac{1}{2}$)=log2$\frac{1}{3}$+$\frac{1}{2}$=$\frac{1}{2}$[1-log29]<0,
所以,x0∈(0,$\frac{1}{2}$),再将区间二等分,中点为$\frac{1}{4}$,
则g($\frac{1}{4}$)=log2$\frac{3}{5}$+$\frac{3}{4}$=$\frac{1}{4}$[3-log2$(\frac{5}{3})^4$]=$\frac{1}{4}$[log28-log2$\frac{625}{81}$]>0,
因此,g($\frac{1}{4}$)•g($\frac{1}{2}$)<0,
所以,存在x0∈($\frac{1}{4}$,$\frac{1}{2}$)使得g(x0)=0,此时区间长度恰好为$\frac{1}{4}$.
点评 本题主要考查了函数奇偶性的判断,二分法,以及对数的运算性质,考查运算求解能力,考查化归与转化思想.属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
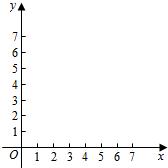 已知函数f(x)=$\left\{\begin{array}{l}{lo{g}_{2}x,x∈[1,4]}\\{(x-5)^{2}+1,x∈(4,7]}\end{array}\right.$.
已知函数f(x)=$\left\{\begin{array}{l}{lo{g}_{2}x,x∈[1,4]}\\{(x-5)^{2}+1,x∈(4,7]}\end{array}\right.$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
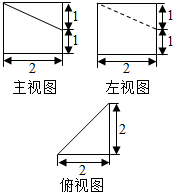
| A. | $\frac{23}{3}$ | B. | 4$\sqrt{2}$+$\sqrt{6}$+6 | C. | 6$\sqrt{2}$+6 | D. | 4$\sqrt{2}$+$\sqrt{6}$+8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com