
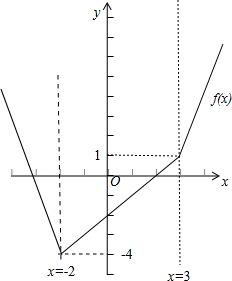
 解:(1)函数f(x)=|2x+4|+|x-3|-9=
解:(1)函数f(x)=|2x+4|+|x-3|-9=
|
| 1 |
| 2 |


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:高中数学 来源: 题型:
| A、若两个变量的线性相关性越强,则相关系数的绝对值越接近于0 |
| B、在某项测量中,测量结果ξ服从正态分布N(1,σ2)(σ>0),若ξ位于区域(0,1)的概率为0.4,则ξ位于区域(1,+∞)内的概率为0.6 |
| C、从匀速传递的产品生产流水线上,质检员每4'分钟从中抽取一件产品进行某项指标检测,这样的抽样是分层抽样 |
| D、利用随机变量Χ2来判断“两个独立事件X,Y的关系”时,算出的Χ2值越大,判断“X与Y有关”的把握就越大 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、f(x)•g(x)>f(a)•g(b) |
| B、f(x)•g(a)>f(a)•g(x) |
| C、f(x)•g(x)>f(b)•g(b) |
| D、f(x)•g(b)>f(b)•g(x) |
查看答案和解析>>
科目:高中数学 来源: 题型:
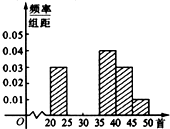 某校开展校园文化活动,其中一项是背诵古诗100首,在该项进行一段时间后,随机抽取40人,统计调查了他们会背古诗的首数,得到的数据如下:
某校开展校园文化活动,其中一项是背诵古诗100首,在该项进行一段时间后,随机抽取40人,统计调查了他们会背古诗的首数,得到的数据如下:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com