
分析 先通过解原不等式知,要使原不等式成立,n最小取8,从而根据数学归纳法的步骤证明原不等式对于任意正整数n≥8成立:1)n=8时成立;2)假设n=k时成立,然后证明n=k+1时成立即可.
解答 证明:根据等比数列求和公式将原不等式变成:$\frac{1-(\frac{1}{2})^{n}}{\frac{1}{2}}>\frac{127}{64}$;
∴$\frac{1}{128}>(\frac{1}{2})^{n}$;
∴要使原不等式成立,n最小取8;
∴(1)n=8时原不等式成立;
(2)假设n=k时原不等式成立,即$1+\frac{1}{2}+\frac{1}{4}+…+\frac{1}{{2}^{k-1}}>\frac{127}{64}$;
∴n=k+1时,$1+\frac{1}{2}+\frac{1}{4}+…+\frac{1}{{2}^{k-1}}+\frac{1}{{2}^{k}}>\frac{127}{64}+\frac{1}{{2}^{k}}$,$\frac{1}{{2}^{k}}>0$;
∴$1+\frac{1}{2}+\frac{1}{4}+…+\frac{1}{{2}^{k}}>\frac{127}{64}$;
即n=k+1时原不等式成立;
∴由(1)(2)知原不等式对于任意正整数n≥8都成立.
由前面知n最小取8;
∴其初始值最小取8.
故答案为:8.
点评 考查等比数列的前n项和公式,以及利用数学归纳法证明命题的步骤,指数式的符号.


 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:高中数学 来源: 题型:选择题
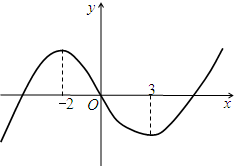
| A. | ($\frac{1}{2}$,+∞) | B. | (-∞,$\frac{1}{2}$) | C. | (-2,3) | D. | (-∞,-2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | A${\;}_{9}^{9}$A${\;}_{2}^{2}$ | B. | A${\;}_{9}^{9}$ | C. | A${\;}_{10}^{10}$ | D. | 2A${\;}_{10}^{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
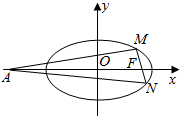 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{6}}}{3}$,焦距为4,定点A(-4,0).
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{6}}}{3}$,焦距为4,定点A(-4,0).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com