Question

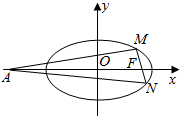
10．已知椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）的离心率为$\frac{{\sqrt{6}}}{3}$，焦距为4，定点A（-4，0）．
（Ⅰ）求椭圆C标准方程；
（Ⅱ）已知P（x₁，y₁），Q（x₂，y₂）是椭圆C上的两点，向量$\overrightarrow m=（{x_1}，\sqrt{3}{y_1}），\overrightarrow n=（{x_2}，\sqrt{3}{y_2}）$，且$\overrightarrow m•\overrightarrow n=0$．设B（x₀，y₀），且$\overrightarrow{OB}=cosθ•\overrightarrow{OP}+sinθ•\overrightarrow{OQ}$（θ∈R），求x₀²+3y₀²的值；
（Ⅲ）如图所示，直线MN经过椭圆C右焦点F．当M、N两点在椭圆C运动时，试判断$\overrightarrow{AM}•\overrightarrow{AN}$×tan∠MAN是否有最大值，若存在求出最大值，并求出这时M、N两点所在直线方程，若不存在，给出理由．

Answer 1

分析 （Ⅰ）根据椭圆的标准方程与几何性质，求出c、a与b的值即可；
（Ⅱ）根据$\overrightarrow m•\overrightarrow n=0$，以及点M满足的条件，求出${{x}_{0}}^{2}$+3${{y}_{0}}^{2}$的表达式并化简即可；
（Ⅲ）由$\overrightarrow{AM}$•$\overrightarrow{AN}$×tan∠MAN=2S_△AMN=|AF||y_M-y_N|，利用直线MN的方程y=k（x-2）与椭圆方程联立，
求出|y_M-y_N|的表达式与最大值，以及对应的直线MN的方程．

解答 解：（Ⅰ）∵椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0），
且离心率e=$\frac{c}{a}$=$\frac{\sqrt{6}}{3}$，焦距2c=4，
∴c=2，a=$\sqrt{6}$；
∴b²=a²-c²=6-4=2，
椭圆C的标准方程为$\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{2}$=1；
（Ⅱ）∵$\overrightarrow m=（{x_1}，\sqrt{3}{y_1}），\overrightarrow n=（{x_2}，\sqrt{3}{y_2}）$，$\overrightarrow m•\overrightarrow n=0$，
∴$\overrightarrow{m}$•$\overrightarrow{n}$=x₁x₂+3y₁y₂=0；
又${{x}_{1}}^{2}$+3${{y}_{1}}^{2}$=6，${{x}_{2}}^{2}$+3${{y}_{2}}^{2}$=6，点M（x₀，y₀），
∴（x₀，y₀）=（x₁cosθ，y₁cosθ）+（x₂sinθ，y₂sinθ）
=（x₁cosθ+x₂sinθ，y₁cosθ+y₂sinθ），
∴${{x}_{0}}^{2}$+3${{y}_{0}}^{2}$=${{（x}_{1}cosθ{+x}_{2}sinθ）}^{2}$+3${{（y}_{1}cosθ{+y}_{2}sinθ）}^{2}$
=（${{x}_{1}}^{2}$+3${{y}_{1}}^{2}$）cos²θ+（${{x}_{2}}^{2}$+3${{y}_{2}}^{2}$）sin²θ+2sinθcosθ（x₁x₂+3y₁y₂）
=6（sin²θ+cos²θ）=6；
（Ⅲ）∵$\overrightarrow{AM}$•$\overrightarrow{AN}$×tan∠MAN=2S_△AMN=|AF||y_M-y_N|，
设直线MN的方程为y=k（x-2），（k≠0）；
联立$\left\{\begin{array}{l}{y=k（x-2）}\\{\frac{{x}^{2}}{6}+\frac{{y}^{2}}{2}=1}\end{array}\right.$，消去x得（1+3k²）y²+4ky-2k²=0，
∴|y_M-y_N|=$\frac{\sqrt{2{4k}^{4}+2{4k}^{2}}}{1+{3k}^{2}}$，
设t=$\frac{\sqrt{2{4k}^{4}+2{4k}^{2}}}{1+{3k}^{2}}$，s=1+3k²，
则t=$\frac{\sqrt{24}•\sqrt{{（\frac{s-1}{3}）}^{2}+（\frac{s-1}{3}）}}{s}$=$\frac{2\sqrt{6}}{3}$•$\sqrt{1+\frac{1}{s}-\frac{1}{{s}^{2}}}$
∴t≤$\sqrt{3}$，当s=4，即k=±1时取等号．
并且，当k=0时$\overrightarrow{AM}$•$\overrightarrow{AN}$×tan∠MAN=0，
当k不存在时|y_M-y_N|=$\frac{2\sqrt{6}}{3}$＜$\sqrt{3}$，
综上，$\overrightarrow{AM}$•$\overrightarrow{AN}$×tan∠MAN有最大值，最大值为6$\sqrt{3}$，
此时，直线MN方程为x-y-2=0，或x+y-2=0．

点评 本题考查了直线与椭圆的综合应用问题，也考查了平面向量的应用问题，考查了构造函数以及求函数的最值问题，是综合性题目．