
分析 (1)设圆G的一般方程为x2+y2+Dx+Ey+F=0,代点可得D、E、F的方程组,解方程组可得;
(2)设直线AD的方程为y=k1(x+5),直线BD的方程为y=k2(x-1),易得k1k2=-1,可得圆的方程为(x-5)2+y2-(10k1-4k2)y-40k1k2=40,令y=0解方程可得定点.
解答 解:(1)设圆G的一般方程为x2+y2+Dx+Ey+F=0,
∵圆G经过点A(-5,0),B(1,0),C(-3,-2$\sqrt{2}$)三点,
∴$\left\{\begin{array}{l}{-5D+F+25=0}\\{D+F+1=0}\\{-3D-2\sqrt{2}E+F+17=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{D=4}\\{E=0}\\{F=-5}\end{array}\right.$
∴圆G的方程为x2+y2+4x-5=0;
(2)∵A(-5,0),B(1,0),
设直线AD的方程为y=k1(x+5),直线BD的方程为y=k2(x-1),
∵D是圆G上异于A,B的任意一点,AB为圆G的直径,∴AD⊥BD,
∴k1k2=-1,又直线AD,BD交直线l:x=5于A′,B′两点,
∴A′(5,10k1),B′(5,4k2),
∴以线段A′B′为直径的圆的圆心为(5,5k1+2k2),半径$\frac{1}{2}$|10k1-4k2|,
∴以线段A′B′为直径的圆的方程为(x-5)2+(y-5k1-2k2)2=$\frac{1}{4}$|10k1-4k2|2,
整理可得(x-5)2+y2-(10k1-4k2)y-40k1k2=40,
令y=0可得(x-5)2=40,解得x1=5+2$\sqrt{5}$,x2=5-2$\sqrt{5}$,
∴以线段A′B′为直径的圆必经过定点(5,5+2$\sqrt{5}$),(5,5-2$\sqrt{5}$)
点评 本题考查直线与圆的位置关系,涉及圆过定点问题,属中档题.


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| Z | 0 | 1 |
| P | 0.75 | 0.25 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
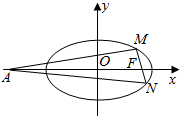 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{6}}}{3}$,焦距为4,定点A(-4,0).
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{6}}}{3}$,焦距为4,定点A(-4,0).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 三边均不相等的三角形 | B. | 直角三角形 | ||
| C. | 等腰非等边三角形 | D. | 等边三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 环数 | 7环以下 | 7 | 8 | 9 | 10 |
| 概率 | 0.13 | a | b | 0.25 | 0.24 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com