
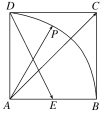
【题目】如图,在正方形ABCD中,E为AB的中点,P为以A为圆心、AB为半径的圆弧上的任意一点,设向量![]() =λ
=λ![]() +μ
+μ![]() ,则λ+μ的最小值为( )
,则λ+μ的最小值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】
以A为原点,以AB所在的直线为x轴,建立直角坐标系,求出向量![]() =(
=( ![]() +μcosθ,﹣λ+μsinθ )=(1,1),用cosθ,sinθ表示 λ和μ,根据cosθ,sinθ 的取值范围,再结合λ+μ的单调性,即可求出范围.
+μcosθ,﹣λ+μsinθ )=(1,1),用cosθ,sinθ表示 λ和μ,根据cosθ,sinθ 的取值范围,再结合λ+μ的单调性,即可求出范围.
以A为原点,以AB所在的直线为x轴,建立直角坐标系,设正方形ABCD的边长为1,
则C(1,1),D(0,1),A(0,0),B(1,0). ![]() E为AB的中点,得
E为AB的中点,得![]()
设 P(cosθ,sinθ),∴![]() =(1,1).
=(1,1).
再由向量![]() =λ(
=λ(![]() ,﹣1)+μ(cosθ,sinθ)=(
,﹣1)+μ(cosθ,sinθ)=(![]() +μcosθ,﹣λ+μsinθ )=(1,1),
+μcosθ,﹣λ+μsinθ )=(1,1),
∴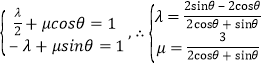 ,
,
∴![]() .由题意得
.由题意得![]() .
.
![]() ,得
,得![]() =
=![]() 0,故λ+μ在[0,
0,故λ+μ在[0,![]() ]上是增函数,
]上是增函数,
当θ=0时,即cosθ=1,这时λ+μ取最小值为![]() ,
,
当θ=![]() 时,即cosθ=0,这时λ+μ取最大值为
时,即cosθ=0,这时λ+μ取最大值为![]() ,
,
故λ+μ的取值范围为[![]() ,5]
,5]
故选:B.


科目:高中数学 来源: 题型:
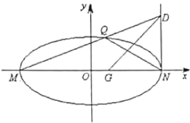
【题目】已知椭圆![]() 经过点
经过点 .离心率
.离心率![]() .
.
(1)求椭圆C的标准方程;
(2)若M,N分别是椭圆长轴的左、右端点,动点D满足![]() ,连接MD交椭圆于点Q.问:x轴上是否存在异于点M的定点G,使得以QD为直径的圆恒过直线QN,GD的交点?若存在,求出点G的坐标;若不存在,说明理由.
,连接MD交椭圆于点Q.问:x轴上是否存在异于点M的定点G,使得以QD为直径的圆恒过直线QN,GD的交点?若存在,求出点G的坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在①离心率![]() ,②椭圆
,②椭圆![]() 过点
过点![]() ,③
,③![]() 面积的最大值为
面积的最大值为![]() ,这三个条件中任选一个,补充在下面(横线处)问题中,解决下面两个问题.
,这三个条件中任选一个,补充在下面(横线处)问题中,解决下面两个问题.
设椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,过
,过![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 交椭圆于
交椭圆于![]() 两点,已知椭圆
两点,已知椭圆![]() 的短轴长为
的短轴长为![]() ,________.
,________.
(1)求椭圆![]() 的方程;
的方程;
(2)若线段![]() 的中垂线与
的中垂线与![]() 轴交于点
轴交于点![]() ,求证:
,求证:![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列选项中,p是q的必要不充分条件的是( )
A.![]() ;
;![]() 方程
方程![]() 的曲线是椭圆
的曲线是椭圆
B.![]() ;
;![]() 对
对![]() 不等式
不等式![]() 恒成立
恒成立
C.设![]() 是首项为正数的等比数列,
是首项为正数的等比数列,![]() 公比小于0;
公比小于0;![]() 对任意的正整数n,
对任意的正整数n,![]()
D.已知空间向量![]() ,
,![]() ,
,![]() ;
;![]() 向量a与b的夹角是
向量a与b的夹角是![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
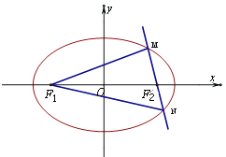
【题目】已知椭圆的焦点坐标为![]() ,
,![]() ,过
,过![]() 垂直于长轴的直线交椭圆于
垂直于长轴的直线交椭圆于![]() 、
、![]() 两点,且
两点,且![]() .
.
(Ⅰ)求椭圆的方程;
(Ⅱ)过![]() 的直线
的直线![]() 与椭圆交于不同的两点
与椭圆交于不同的两点![]() 、
、![]() ,则
,则![]() 的内切圆的面积是否存在最大值?若存在求出这个最大值及此时的直线方程;若不存在,请说明理由.
的内切圆的面积是否存在最大值?若存在求出这个最大值及此时的直线方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面内一动点![]() (
(![]() )到点
)到点![]() 的距离与点
的距离与点![]() 到
到![]() 轴的距离的差等于1,
轴的距离的差等于1,
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过点![]() 的直线
的直线![]() 与轨迹
与轨迹![]() 相交于不同于坐标原点
相交于不同于坐标原点![]() 的两点
的两点![]() ,求
,求![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国家统计局进行第四次经济普查,某调查机构从15个发达地区,10个欠发达地区,5个贫困地区中选取6个作为国家综合试点地区,然后再逐级确定普查区域,直到基层的普查小区.普查过程中首先要进行宣传培训,然后确定对象,最后入户登记,由于种种情况可能会导致入户登记不够顺利,这为正式普查提供了宝贵的试点经验,在某普查小区,共有50家企事业单位,150家个体经营户,普查情况如下表所示:
普查对象类别 | 顺利 | 不顺利 | 合计 |
企事业单位 | 40 | 10 | 50 |
个体经营户 | 90 | 60 | 150 |
合计 | 130 | 70 | 200 |
(1)写出选择6个国家综合试点地区采用的抽样方法;
(2)根据列联表判断是否有97.5%的把握认为“此普查小区的入户登记是否顺利与普查对象的类别有关”,分析造成这个结果的原因并给出合理化建议.
附:参考公式:![]() ,其中
,其中![]()
参考数据:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com