
| A�� | [-2��1] | B�� | [-5��1] | C�� | [-2��4] | D�� | [-5��4] |
���� ����ͼ��ĶԳ����ĵ��Գ������С����Ϊ$\frac{��}{4}$���ɵ�����T=�У�����أ����ú���y=Asin����x+�գ���ͼ��任���ɣ����g��x����x��[0��$\frac{��}{3}$]�ϣ����g��x����Χ���ɵ�m�ķ�Χ��
��� �⣺�����⣬ͼ��ĶԳ����ĵ��Գ������С����Ϊ$\frac{��}{4}$��
������T=����$\frac{2��}{��}=��$
���=2��
��f��x��=$\sqrt{3}$sin��2x-$\frac{��}{6}$��-$\frac{1}{2}$��
f��x����ͼ������ƽ��$\frac{��}{12}$����λ���ȣ��õ���$\sqrt{3}$sin��2x-$\frac{��}{6}$-$\frac{��}{6}$��-$\frac{1}{2}$=$\sqrt{3}$sin��2x-$\frac{��}{3}$��$-\frac{1}{2}$=g��x����
��x��[0��$\frac{��}{3}$]�ϣ�
��2x-$\frac{��}{3}$��[$-\frac{��}{3}$��$\frac{��}{3}$]
sin��2x-$\frac{��}{3}$����[$-\frac{\sqrt{3}}{2}$��$\frac{\sqrt{3}}{2}$]
��g��x����[-2��1]
Ҫʹg��x��-3��m��g��x��+3��x��[0��$\frac{��}{3}$]�Ϻ������
��1-3��m��-2+3��
�ɵã�-2��m��1��
��ѡA��
���� ������Ҫ�������Ǻ��������������ʽ������y=Asin����x+�գ���ͼ��任���ɣ������������ת��Ϊ��ֵΪ�������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
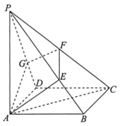 ��ͼ��������P-ABCD�У�����ABCDΪ�����Σ�PA�A����ABCD��PA=AC������A��ƽ������PB��PC��PD�ֱ��ڵ�E��F��G��E��F��G�����������Ķ˵㴦����
��ͼ��������P-ABCD�У�����ABCDΪ�����Σ�PA�A����ABCD��PA=AC������A��ƽ������PB��PC��PD�ֱ��ڵ�E��F��G��E��F��G�����������Ķ˵㴦�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a��b��c | B�� | c��b��a | C�� | b��a��c | D�� | c��a��b |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ϲ������ | ��ϲ������ | �ϼ� | |
| 90�� | 20 | 5 | 25 |
| 80�� | 10 | 15 | 25 |
| �ϼ� | 30 | 20 | 50 |
| P��K2��k0�� | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
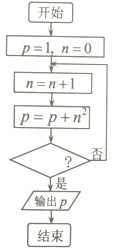
| A�� | n��2 | B�� | n��3 | C�� | n��4 | D�� | n��5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
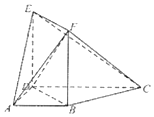 ��ͼ������ABCD�У���BAD=��ADC=90�㣬CD=2��AD=AB=1���ı���BDEFΪ�����Σ���ƽ��BDEF�Aƽ��ABCD
��ͼ������ABCD�У���BAD=��ADC=90�㣬CD=2��AD=AB=1���ı���BDEFΪ�����Σ���ƽ��BDEF�Aƽ��ABCD�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com