
| A. | $\frac{π}{2}$ | B. | π | C. | 2π | D. | 4π |
分析 f(x)=$\overrightarrow{OA}$•$\overrightarrow{OB}$,根据平面向量数量积运算,求解出f(x)化简,再利用周期公式求函数的最小正周期.
解答 解:$\overrightarrow{OA}$=(cos2x,-1),$\overrightarrow{OB}$=(1,sin2x+$\sqrt{3}$sin2x),
那么:f(x)=$\overrightarrow{OA}$•$\overrightarrow{OB}$=cos2x-sin2x-$\sqrt{3}$sin2x=cos2x-$\sqrt{3}$sin2x=2cos(2x+$\frac{π}{3}$).
函数f(x)的最小正周期T=$\frac{2π}{2}=π$,
故选:B.
点评 本题主要考查对三角函数的化简能力和三角函数的图象和性质的运用,利用三角函数公式将函数进行化简是解决本题的关键.属于基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(π)<f(3)<f($\sqrt{2}$) | B. | f(π)<f($\sqrt{2}$)<f(3) | C. | f($\sqrt{2}$)<f(3)<f(π) | D. | f($\sqrt{2}$)<f(π)<f(3) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
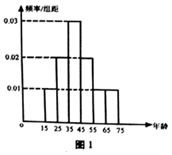 持续性的雾霾天气严重威胁着人们的身体健康,汽车的尾气排放是造成雾霾天气的重要因素之一.为此,某城市实施了机动车尾号限行,该市报社调查组为了解市区公众对“车辆限行”的态度,随机选取了30人进行调查,将他们的年龄(单位:岁)数据绘制成频率分布直方图(图1),并将调查情况进行整理后制成表2:
持续性的雾霾天气严重威胁着人们的身体健康,汽车的尾气排放是造成雾霾天气的重要因素之一.为此,某城市实施了机动车尾号限行,该市报社调查组为了解市区公众对“车辆限行”的态度,随机选取了30人进行调查,将他们的年龄(单位:岁)数据绘制成频率分布直方图(图1),并将调查情况进行整理后制成表2:| 年龄(岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75] |
| 频数 | 3 | 6 | 6 | 3 | ||
| 赞成人数 | 2 | 4 | 5 | 4 | 2 | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 定义[x]表示不超过x的最大整数,例如[2.11]=2,[-1.39]=-2,执行如下图所示的程序框图,则输出m的值为
定义[x]表示不超过x的最大整数,例如[2.11]=2,[-1.39]=-2,执行如下图所示的程序框图,则输出m的值为| A. | $\frac{19}{3}$ | B. | $\frac{53}{8}$ | C. | $\frac{171}{6}$ | D. | $\frac{185}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\sqrt{2}$ | C. | $\frac{5}{2}$ | D. | $\frac{5\sqrt{2}}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com