
分析 由条件求得|$\overrightarrow{OP}$|、$\overrightarrow{OA}•\overrightarrow{OP}$的值,可得$\overrightarrow{OA}$在$\overrightarrow{OP}$上的投影为x=$\frac{λ}{\sqrt{{5λ}^{2}-8λ+4}}$,分类讨论,求得$\frac{1}{x}$的范围,可得x的范围.
解答 解:∵|$\overrightarrow{OA}$|=1,|$\overrightarrow{OB}$|=2,$\overrightarrow{OA}$•$\overrightarrow{OB}$=0,$\overrightarrow{OP}$=λ$\overrightarrow{OA}$+μ$\overrightarrow{OB}$,且λ+μ=1,
∴|$\overrightarrow{OP}$|=$\sqrt{{[λ\overrightarrow{OA}+(1-λ)\overrightarrow{OB}]}^{2}}$=$\sqrt{{λ}^{2}+0+{4(1-λ)}^{2}}$=$\sqrt{{5λ}^{2}-8λ+4}$,
∴$\overrightarrow{OA}$•$\overrightarrow{OP}$=$\overrightarrow{OA}$•[λ$\overrightarrow{OA}$+(1-λ)$\overrightarrow{OB}$]=λ•${\overrightarrow{OA}}^{2}$+(1-λ)$\overrightarrow{OA}$•$\overrightarrow{OB}$=λ•${\overrightarrow{OA}}^{2}$=λ.
设$\overrightarrow{OA}$在$\overrightarrow{OP}$上的投影为x,则 $\overrightarrow{OA}$•$\overrightarrow{OP}$=x•|$\overrightarrow{OP}$|=x•$\sqrt{{5λ}^{2}-8λ+4}$=λ,
∴x=$\frac{λ}{\sqrt{{5λ}^{2}-8λ+4}}$.
当λ=0时,x=0,当λ>0时,$\frac{1}{x}$=$\sqrt{\frac{{5λ}^{2}-8λ+4}{{λ}^{2}}}$=$\sqrt{\frac{4}{{λ}^{2}}-\frac{8}{λ}+5}$=$\sqrt{{(\frac{2}{λ}-2)}^{2}+1}$,故当λ=1时,$\frac{1}{x}$取得最小值,为1,
即$\frac{1}{x}$≥1,∴0<x≤1.
当λ<0时,$\frac{1}{x}$=-$\sqrt{\frac{{5λ}^{2}-8λ+4}{{λ}^{2}}}$=-$\sqrt{\frac{4}{{λ}^{2}}-\frac{8}{λ}+5}$=-$\sqrt{{(\frac{2}{λ}-2)}^{2}+1}$<-$\sqrt{4+1}$=-$\sqrt{5}$,即 $\frac{1}{x}$<-$\sqrt{5}$,
∴-$\sqrt{5}$<x<0.
综上可得,x∈(-$\sqrt{5}$,1],
故答案为:(-$\sqrt{5}$,1].
点评 本题考点是向量在几何中的应用,综合考查了向量的线性运算,向量的数量积的运算及数量积公式,熟练掌握向量的相关公式是解题的关键,是中档题.


 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|0≤x≤1} | B. | {x|1<x<2} | C. | {x|0≤x<2} | D. | {x|0≤x≤1}∪{2} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2π2a3 | B. | π2a3 | C. | $\frac{{π}^{2}}{2}$a3 | D. | $\frac{{π}^{2}}{3}$a3 |
查看答案和解析>>
科目:高中数学 来源:2016-2017学年广东清远三中高一上学期月考一数学试卷(解析版) 题型:选择题
已知函数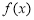 的定义域为
的定义域为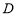 ,若对任意
,若对任意 ,当
,当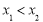 时,都有
时,都有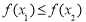 ,则称函数
,则称函数 在
在 上为非减函数.设函数
上为非减函数.设函数 在
在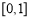 上为非减函数,且满足以下三个条件:①
上为非减函数,且满足以下三个条件:① ;②
;② ;③
;③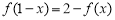 .则
.则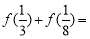 ( )
( )
A. 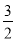 B.
B.  C.
C.  D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com