
| 年份 | 2011 | 2012 | 2013 | 2014 | 2015 |
| 居民生活用水量(万吨) | 236 | 246 | 257 | 276 | 286 |
分析 (I)根据回归系数公式计算回归系数,得出回归方程;
(II)由于到2020年用水量趋于稳定,故2023年的用水量约等于2020年的用水量,把x=2020代入回归方程求出用水量的估计值.
解答 解:(I)$\overline{x}$=2013,$\overline{y}$=$\frac{236+246+257+276+186}{5}$=260.2,
$\sum_{i=1}^{5}({x}_{i}-\overline{x})({y}_{i}-\overline{y})$=(-2)×(-24.2)+(-1)×(-14.2)+0+1×15.8+2×25.8=130.
$\sum_{i=1}^{5}({x}_{i}-\overline{x})^{2}$=4+1+0+1+4=10.
∴b=$\frac{130}{10}$=13,
∴回归方程为y-260.2=13(x-2013),即y=13(x-2013)+260.2.
(II)当x=2020时,y=13(2020-2013)+260.2=351.2(万吨).
答:该城市2023年的居民生活用水量预计为351.2万吨.
点评 本题考查了线性回归方程的求解并利用回归方程进行预测,属于中档题.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:高中数学 来源: 题型:解答题
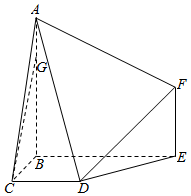 如图,多面体ABCDEF中,BA,BC,BE两两垂直,且AB∥EF,CD∥BE,AB=BE=2,BC=CD=EF=1.
如图,多面体ABCDEF中,BA,BC,BE两两垂直,且AB∥EF,CD∥BE,AB=BE=2,BC=CD=EF=1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 连锁店 | A店 | B店 | C店 | |||
| 售价x(元) | 80 | 86 | 82 | 88 | 84 | 90 |
| 销售量y(件) | 88 | 78 | 85 | 75 | 82 | 66 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 6 | 8 | 10 | 12 |
| y | 6 | m | 3 | 2 |
| A. | 变量x,y之间呈现负相关关系 | |
| B. | m=4 | |
| C. | 可以预测,当x=11时,y=2.6 | |
| D. | 由表格数据知,该回归直线必过点(9,4) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ②③ | B. | ②③④ | C. | ①③④ | D. | ③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com