
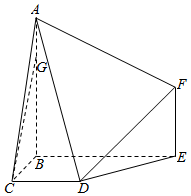
 如图,多面体ABCDEF中,BA,BC,BE两两垂直,且AB∥EF,CD∥BE,AB=BE=2,BC=CD=EF=1.
如图,多面体ABCDEF中,BA,BC,BE两两垂直,且AB∥EF,CD∥BE,AB=BE=2,BC=CD=EF=1.分析 (I)分别取AB,AF的中点M,H,连结MF,GH,DH,则由中位线定理可得GH$\stackrel{∥}{=}$$\frac{1}{2}$MF$\stackrel{∥}{=}$$\frac{1}{2}$BE,又CD$\stackrel{∥}{=}$$\frac{1}{2}BE$,得出四边形CDHG是平行四边形,故CG∥DH,从而CG∥平面ADF;
(II)将多面体分解成三棱锥A-BCD和四棱锥D-ABEF,分别计算体积即可.
解答  解:(Ⅰ)分别取AB,AF的中点M,H,连结MF,GH,DH.
解:(Ⅰ)分别取AB,AF的中点M,H,连结MF,GH,DH.
∵EF$\stackrel{∥}{=}$BM=$\frac{1}{2}AB$,
∴四边形BEFM是平行四边形,
∴MF$\stackrel{∥}{=}$BE.
∵G,H分别是AM,AF的中点,
∴$GH\underline{\underline∥}\frac{1}{2}MF$$\stackrel{∥}{=}$$\frac{1}{2}BE$,
又∵CD$\stackrel{∥}{=}$$\frac{1}{2}$BE,
∴$CD\underline{\underline∥}GH$,
∴四边形CDHG是平行四边形
∴CG∥DH,又∵CG?平面ADF,DH?平面ADF
∴CG∥平面ADF
(Ⅱ)∵BA,BC,BE两两垂直,
∴AB⊥平面BCDE,BC⊥平面ABEF.
VA-BCD=$\frac{1}{3}{S}_{△BCD}•AB$=$\frac{1}{3}×\frac{1}{2}×1×1×2$=$\frac{1}{3}$.
VD-ABEF=$\frac{1}{3}{S}_{梯形ABEF}•BC$=$\frac{1}{3}×\frac{1}{2}×(1+2)×2×1$=1.
∴多面体ABCDEF的体积V=VA-BCD+VD-ABEF=$\frac{4}{3}$.
点评 本题考查了线面平行的判定,棱锥的体积计算,属于中档题.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:高中数学 来源: 题型:选择题
| A. | 1cm | B. | 2cm | C. | 3cm | D. | $\sqrt{3}$cm |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | [1,+∞) | C. | [2,+∞) | D. | (-∞,0]∪[1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | -6 | C. | $-\frac{10}{3}$ | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 60° | C. | 30°或150° | D. | 60°或120° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年份 | 2011 | 2012 | 2013 | 2014 | 2015 |
| 居民生活用水量(万吨) | 236 | 246 | 257 | 276 | 286 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com